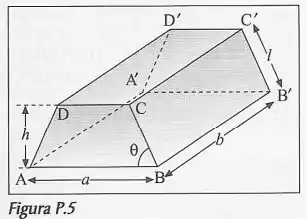
Um reservatório tem a forma de um prisma, cujas faces A B C D e A’ B’ C’ D’ são trapézios isósceles com as dimensões indicadas na fig P.5; as demais faces são retangulares. O reservatório está cheio até o topo de um líquido com densidade .
(a) Calcule a força total exercida pelo líquido sobre a base do reservatório.
(b) Calcule a resultante das forças exercidas pelo líquido sobre todas as paredes do reservatório e compare-a com o peso total do líquido. Analise o resultado como ilustração do paradoxo hidrostático (seç.1.6)
Passo 1
Fala ai galerinha bonita, tudo beleza? Nessa questão aqui, o enunciado nos diz que temos um reservatória num formato de prisma como dado na figura a seguir:
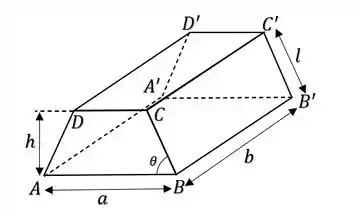
O reservatório está cheio até o topo com um liquido de densidade , e sabendo disso o enunciado nos pede primeiro pra encontrar a força total exercida pelo líquido sobre a base do reservatório.
Passo 2
Dessa maneira podemos lembrar da relação entre a força e a pressão que ela exerce sobre uma área :
Logo:
E como a Lei de Stevin nos diz que pressão que uma coluna de liquido exerce depende apenas da gravidade da altura da coluna e da densidade , temos que:
Onde é a altura do prisma. Enquanto que a área da base será dada como:
Portanto a força que o liquido exerce sobre a base do reservatório é dada como:
E como a força é exercida diretamente sobre a base, a sua direção é na vertical para baixo
Passo 3
Agora na letra (b), queremos encontrar a resultante das forças que o liquido exerce sobre as paredes do reservatório. Nesse caso, a primeira malandragem que devemos perceber é que as forças que o liquido exerce nas paredes que NÃO estão inclinadas (as paredes cuja área é o trapézio) se anulam, já que apontam em sentidos opostos.
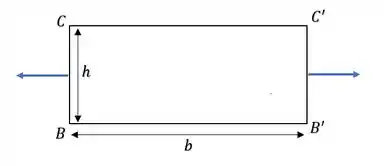
Dessa maneira precisamos analisar somente as forças que atuam nas paredes inclinadas:
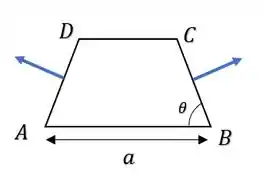
Sendo assim, a força na parede inclinada pode ser decomposta em cada eixo, de maneira que as componentes horizontais da forças se anulam, sobrando somente as componentes verticais das forças.
Ou seja, com essa informação, conseguimos descobrir que a resultante da força que liquido exerce sobre as paredes do reservetória possui direção vertical e aponta pra cima.
MAAAASSSSS, a malandragem é exatamente essa, porque afinal o reservatório não sai voando pra cima com a força do liquido, ele fica parado, de maneira que nos faz pensar que existe alguma outra força de mesmo módulo e direção mas com sentido contrário, E NÓS CONHECEMOS ESSA FORÇA!
É a própria força peso do liquido, ou seja, a resultante da força que o liquido exerce sobre as paredes do reservatório vai ser IGUAL AO PESO DO LIQUIDO NAQUELE PONTO.
Passo 4
Sendo assim, pra gente encontrar a resultante , devemos encontrar o peso do liquido.
Onde é a massa do liquido. Podemos expressar a massa como:
Onde é a densidade do liquido enquanto que é o volume do reservatório. Nesse sentido, o volume pode ser expresso como o produo entre a área da base (área do trapézio) pelo comprimento do reservatório :
Temos o trapézio dado como:
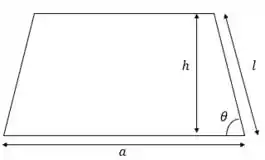
Em que sua área pode ser expressa como:
A base maior o enunciado nos deu valendo como , e a altura é dada como então precisamos encontrar somente a base menor, na imagem vamos chama-la de , tal que:
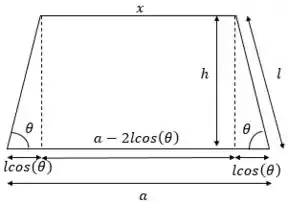
Logo, teremos que:
Portanto:
Podemos colocar o em evidência:
E
Passo 5
Show de bolinhas, então podemos dizer que o volume do liquido no reservatório é dado como:
Então a massa do liquido presente dentro desse reservatório será:
Portanto, o peso do liquido e consequente a resultante das forças na parede será: