Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 32.Exercícios e Problemas - Ex. 25
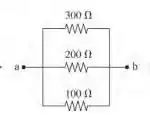
Qual é a resistência equivalente entre os pontos a e b da FIGURA EX32.25?
Passo 1
Falaaa, cara, tranquileba?
Temos 2 linhas com circuitos em serie, fazendo ambos teremos os três formando em paralelo, E nessa ordem assim faremos.
Pode parecer confuso, mas chega comigo que faremos juntos!!
Passo 2
Para o primeiro, temos 3 resistores em série, os três contendo . Assim, essa resistência equivalente de resistores em série é de:
Assim:
E na segunda linha do circuito temos outra sequência de resistores em série. Assim:
Assim ficando:
Passo 3
Agora temos um circuito com resistores em paralelo, e sabemos que para resistores em paralelo a resistência equivalente é dada por:
Logo:
Assim ficando:
Assim a resistência total entre a ligação entre a e b é de