1. Considerando que a corda é enrolada ao redor de duas roldanas leves e sem atrito, que são separadas por uma distância d, a tensão na corda são as forças que agem na direção das roldanas, como mostrado na figura a seguir, e pode ser determinada através do somatório de forças no eixo y. S e o sistema está em equilíbrio, temos que o somatório de forças em y é .



Passo 3

Fazendo o somatório de forças em y temos que a tensão na corda é dada por:

Sabe-se que a corda tem no total L metros, somando os três lados do triângulo formado. Se d é igual a d metros, os outros dois lados devem ter d metros no total, sendo metros, com cada um valendo , como pode ser visto na figura a seguir. Sabendo o comprimento dos lados, podemos, por trigonometria, determinar o valor do ângulo ;



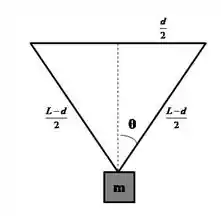
Nessa figura, a medida do comprimento da corda nos lados do triangulo formado:

Passo 4

Para substituirmos na equação (3) precisamos encontrar . Pelas relações trigonométricas e substituindo o valor de , temos:

Passo 5

Sabendo o valor do ângulo, determinado anteriormente, podemos pela equação (3) determinar então a tensão na corda:

Passo 6

2. Para determinarmos a frequência com que a corda deve vibrar devemos, primeiro, determinar a velocidade das ondas na corda, partindo da equação (1):

Considerando o comprimento d a corda fez três loops. Dessa maneira, podemos , então, fazer a seguinte relação:

Substituindo a velocidade e o comprimento na equação (2), podemos determinar a frequência da corda entre as roldanas como sendo: