Uma roda de raio R rola ao longo de um plano horizontal. Prove que, em cada instante, a velocidade de cada ponto é perpendicular à reta que une o ponto com o ponto ele contato ela roda com o plano. Se p é a distância entre esses pontos, prove que o módulo da velocidade elo ponto móvel é wp. O que se pode concluir desses resultados?
Passo 1
Opaaa tudo bem?
Vamos lá para mais um problema bem legal ein!
Passo 2
Vou fazer um desenho esquemático pra ficar mais fácil de a gente observar, beleza?
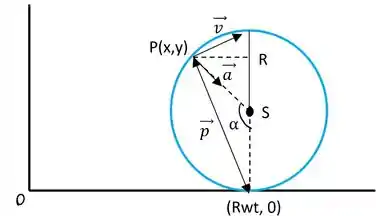
Passo 3
A velocidade resultante é a soma da velocidade das duas direções, e
Como visto na questão anterior, as velocidades nas direções podem ser definidas como
Então, temos que a velocidade é dada por
Passo 4
A distância entre os pontos é definida como
Passo 5
Quando dois vetores são perpendiculares, o produto vetorial entre eles é igual à zero. Então podemos fazer o produto vetorial entre o vetor distância entre os pontos e o vetor velocidade
Então, como o produto vetorial entre os vetores é igual à zero, os vetores são perpendiculares.
Passo 6
O módulo de um dado vetor é dado por
Então, para o módulo do vetor velocidade temos
Uma propriedade de ciclo trigonométrico importante é dada por
E podemos aplicar essa propriedade na equação do módulo de velocidade
Passo 7
Também podemos obter o módulo do vetor distância dos pontos ()
Passo 8
Das duas equações obtidas, podemos concluir que
Passo 9
Podemos observar algumas coisas importantes desse problema
- A velocidade é máxima quando
- A velocidade é zero quando está na horizontal
- A velocidade sempre está apontando ao ponto de altura máxima (para que o ângulo sem inserido, será sempre reto)
- A aceleração está em direção ao centro
Resposta
Ei, a resposta está no passo a passo :)