Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Mecânica- Ed: 2º - Capítulo 5.Problemas - Ex. 67

Uma metralhadora dispara um projétil com uma velocidade de 220   m / s . Determine o ângulo de disparo para que o projétil atinja um alvo ela altura 6   m , à distância de 150   m .

Passo 1

Este é um típico problema de lançamento obliquo. O primeiro passo é fazer um desenho que ilustre bem a situação:

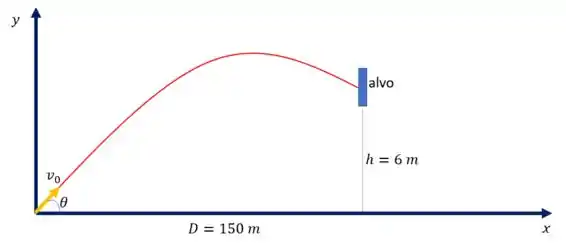
Daí, decompomos o vetor velocidade inicial:

v 0 x = v 0 cos ⁡ θ               e             v 0 y = v 0   s e n   θ

Nosso objetivo é achar o ângulo θ !

Passo 2

Na vertical, temos um movimento uniformemente acelerado:

y = y 0 + v 0 y t + a t 2 2

Como y 0 = 0 , v 0 y = v 0   s e n   θ e a = - g , temos que

y = v 0   s e n   θ   t - g t 2 2

Já na horizontal, o movimento é uniforme:

x = x 0 + v x t = 0 + v 0 cos ⁡ θ   t

Daí,

t = x v 0 cos ⁡ θ

Substituindo na equação para y :

y = v 0   s e n   θ x v 0 cos ⁡ θ - g 2 ⋅ x 2 v 0 2 cos 2 ⁡ θ

Portanto, a trajetória parabólica é descrita pela equação

y = x tan ⁡ θ - g 2   v 0 2 cos 2 ⁡ θ x 2

Passo 3

Vamos substituir g = 9,8   m / s 2 e v 0 = 220   m / s :

y = x tan ⁡ θ - 9,8 2 ⋅ 220 2 ⋅ x 2 cos 2 ⁡ θ

Aqui vem o pulo do gato: quando x = 150   m , temos y = 6   m :

6 = 150 tan ⁡ θ - 9,8 2 ⋅ 220 2 ⋅ 150 2 cos 2 ⁡ θ

6 150 = tan ⁡ θ - 4,9 ⋅ 15 22 0 ⋅ 22 ⋅ sec 2 ⁡ θ  

Logo, como 1 + tan 2 ⁡ θ = sec 2 ⁡ θ :

1 25 = tan ⁡ θ - 73,5 22 0 ⋅ 22 1 + tan 2 ⁡ θ

Por simplicidade, vamos chamar u = tan ⁡ θ :

1 25 + 73,5 22 0 ⋅ 22 = u - 73,5 22 0 ⋅ 22 u 2

Ou ainda,

u 2 - 65,85 u + 3,63 = 0

As soluções dessa equação são

u = 0,055               e             u = 65,8

Com isso, temos

tan ⁡ θ = 0,055 → θ = 3,15 °

tan ⁡ θ = 65,8 → θ = 89,1 °

Essas duas respostas são possíveis, porém a situação com 3,15 ° é mais factível...

Resposta

3,15 °             o u         89,1 °

Ver Outros Exercícios desse livro