Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 33.Exercícios e Problemas - Ex. 14
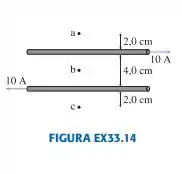
Quais são a intensidade e a orientação do campo magnético nos pontos de a até c da FIGURA EX33.14?
Passo 1
Faaaaaala, galera... Tranquileba??
Para que saibamos o campo magnético, primeiro saber como ele é, certo?! E para um fio temos então, neste caso, é essencial, então vamos acha-lo!
Sabemos que a lei de Bio-Savart é:
E para um fio muito longo, como:
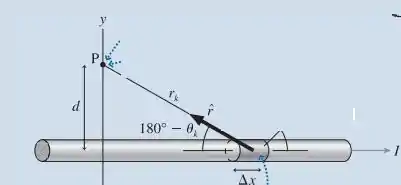
Temos que:
E:
Assim:
Sendo um fio muito longo, logo:
Logo:
De integral simples. Assim, o campo elétrico a uma distancia d sobre um fio longo que passa uma corrente é:
Com esse “insight” nem precisa mais de mim, né?! Mas se gosta de mim, cola pro próximo passo!
Passo 2
Gostou né?! huehue
Brincadeiras à parte, pede-se B. E para os pontos, podemos usar o principio da superposição.
Passo 3
Tem se que a corrente do fio mais próximo aponta para a direita, e a do fio mais longe, esquerda. Assim, tomemos o eixo x positivo para a direita. De modo que ao fio mais próximo gera um campo magnético que aponta para fora da página , e o do fio mais longe, para dentro da página .
Para o ponto a)
Concluímos que:
Para o ponto b)
Visto de cima, veja que o ponto b tem uma corrente passando a sua direita indo para cima, e uma à sua esquerda, indo para baixo. Logo elas se somam! E ambas entrando na página para b
Concluímos que:
Para o ponto c)
Mesmo pensamento para o ponto a e mesma distancia logo:
Resposta
Saindo da página
Entrando na página.