Enunciado
Física - Eisberg e Resnick - Física quântica- Ed: 1º - Capítulo 5.Problemas - Ex. 9
a) Seguindo o processo do exemplo 5-9, verifique que a função de onda
é uma solução para a equação de Schroedinger na região , para uma partícula que se move livremente nessa região, mas que está estritamente confinada a ela.
b) Determine também o valor da energia total da partícula nesse primeiro estado excitado do sistema, e compare com a energia total do estado fundamental obtida no exemplo 5-9.
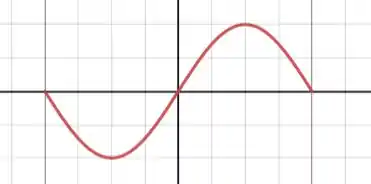
c) Trace um gráfico da dependência espacial dessa função de onda.
Passo 1
Fala galerinha, beleza?
Precisamos mostrar que essa função de onda é solução da equação de Schroedinger
Como a partícula é livre dentro da caixa, temos
Além disso, as condições de contorno devem ser
Como , isso é verificado facilmente, basta substituir!
Passo 2
Mas ainda falta mostra que a função de onda é solução da equação. Para isso, vamos tomar as derivadas:
Agora substituímos na equação com potencial nulo:
Assim
Desta forma, vemos que é solução da equação de Schroedinger se a energia for dada por
Isso já resolve os itens (a) e (b)!
Passo 3
Para analisar o comportamento espacial da função de onda, basta plotar a função :
