Enunciado
Física - Okuno - Física para Ciências Biológicas e Biomédicas- Ed: 1º - Capítulo 14.Problemas - Ex. 11
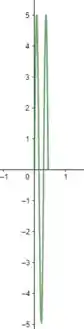
Seja uma onda estacionaria com quatro nós, dois dos quais situados nas extremidades fixas (terceira harmônica), numa corda de violão de 45 cm de comprimento. No instante t = 0 o deslocamento vertical do ventre é máximo e vale 5 cm. Desenhe a forma da onda para os instantes
Passo 1
E aíiíí cara! Vamos pra mais uma de ondas
Antes de tudo, dá uma olhada lá no exercício resolvido 14.3 do seu livro. Ali, ele já nos deu de bandeja que a velocidade da onda em uma corda de violão é
Outra coisa que já temos do enunciado do exercício é o comprimento de onda, porque olha só: se temos uma terceira harmônica, temos uma onda e meia em de corda, portanto, o comprimento de uma onda será:
Também temos a amplitude , que vale
Para descobrirmos a frequência , vamos usar:
Portanto, a frequência angular é
E o período é
E o número de onda é dado por
Agora é só substituir as informações nessa equação:
Passo 2
A equação geral de onda é
Substituindo as informações que encontramos:
Belezinha, agora vamos desenhar a configuração dessa onda para os seguintes valores de :
Vamos lá!
Passo 3
Para
Se , temos:
Uma onda de amplitude que vai ter seus nós nos seguintes valores de :
Então temos:
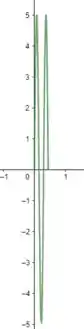
Passo 4
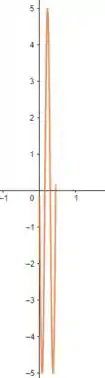
Para
Se , temos:
Então temos:
Passo 5
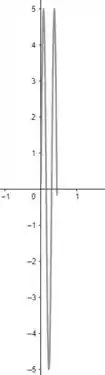
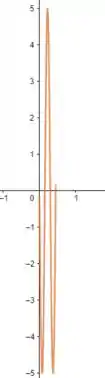
Para
Se , temos:
Então temos:
Passo 6
Para
Se , temos:
Então temos:
Passo 7
Para
Se , temos:
Então temos: (como é o período, aqui temos a mesma onda de )
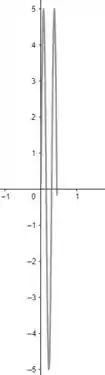
Resposta
