Seja a secção longitudinal de um diamante lapidado, cujo índice de refração vale 2,4. Um feixe luminoso incide sobre a face A E perpendicularmente.a. Determine a trajetória desse feixe até que ele saia do cristal. Justifique.b. Qual deve ser o maior ângulo de incidência na face A E de forma que ainda ocorra reflexão total na face BC?c. Um diamante lapidado é chamado brilhante. Esse nome é justificável?
Passo 1
a. Primeiramente é preciso ver se vai ocorrer reflexão total na face BC.
Condição para que ocorra reflexão total:
Logo, se o ângulo de incidência for superior a 24,62° ocorre reflexão total, e como nosso ângulo é de 45°, então podemos afirmar que irá ocorrer e o sistema se comportará conforme a figura abaixo.
Passo 2
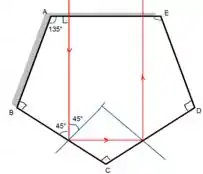
b. Da geometria da figura abaixo podemos descobrir o valor de , sabendo que da condição de reflexão total da letra a.
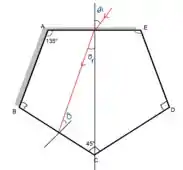
Se
E a soma de todos os ângulos de um triângulo é 180°, então:
Logo,
Usando a lei de snell na normal da face AE:
Passo 3
c. Sim, pois em suas faces os raios de luz sofrem reflexão total quando a luz incide perpendicularmente neles e assim a luz reflete pros olhos do observador gerando o efeito de brilho.
Resposta
a.
b.
c. Sim, pois em suas faces os raios de luz sofrem reflexão total quando a luz incide perpendicularmente neles e assim a luz reflete pros olhos do observador gerando o efeito de brilho.