Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.Problemas Adicionais - Ex. 75
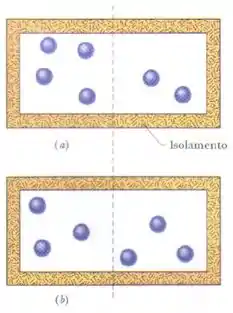
O sistema de três partículas e o sistema de cinco partículas estão em caixas isoladas como as da figura. Qual é a menor multiplicidade (a) do sistema e (b) do sistema ? Qual é a maior multiplicidade (c) do sistema e (d) do sistema ? Qual é a maior entropia (e) do sistema e (f) do sistema ?
Passo 1
(a) Nesse caso da caixa com um certo número de partículas em cada lado, a fórmula da multiplicidade é:
Onde e são as quantidades de partículas em cada lado da caixa.
No caso do sistema , como , a menor multiplicidade acontece quando todas as partículas estão do mesmo lado, ou seja:
Passo 2
(b) No caso do sistema , como , a menor multiplicidade também acontece quando todas as partículas estão do mesmo lado, ou seja:
Esse é o caso porque o objetivo é fazer o denominador ficar o maior possível, e como o fatorial cresce muito rápido, é melhor fazer o maior número possível aparecer dentro do fatorial.
Passo 3
(c) Agora é só inverter essa lógica. Como o fatorial cresce muito rápido, e queremos ter o menor denominador possível, precisamos fazer os menores números aparecem dentro do fatorial.
No caso do sistema , isso quer dizer que:
Passo 4
(d) E no caso do sistema :
Passo 5
(e) Pra saber a maior entropia, é só calcular o valor no caso de maior multiplicidade.
No caso do sistema :
Passo 6
(e) E no caso do sistema :
Resposta
(a)
(b)
(c)
(d)
(e)
(f)