Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 4.1 - Ex. 2
Para soltar uma caminhonete presa na lama, trabalhadores usam três cordas horizontais, produzindo os vetores de força mostrados na Figura . (a) Ache os componentes e de cada um dos três puxões. (b) Use os componentes para achar o módulo, a direção e o sentido do resultante dos três puxões.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar (a) os componentes e de cada uma das três forças e (b) o módulo, a direção e o sentido da força resultante no sistema da figura abaixo:
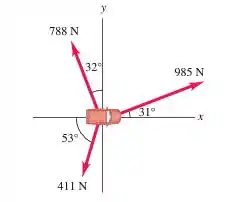
Então, conhecemos as magnitudes e direções de três vetores () e queremos usá-los para encontrar seus componentes, e então usar os componentes para encontrar a magnitude e direção do vetor resultante.
Nós sabemos que os componentes da força são dados por:
E que a força resultante tem seu módulo calculado na forma:
Com direção . No nosso caso, os ângulos que as forças fazem com o eixo são:
Então, vamos calcular o que se pede com base nesses dados. Vamos lá!
Passo 2
a) Vamos encontrar as componentes em e de cada força, com base na geometria formada pelos vetores e ângulos fornecidos. Assim, temos:
Para a força , que forma um ângulo com a horizontal:
Para a força , que forma um ângulo com a vertical:
E para a força , que forma um ângulo com a horizontal:
Então, encontramos todas as componentes.
Passo 3
b) Agora vamos calcular a força resultante no eixo e no eixo , usando os resultados obtidos no passo anterior. Assim, temos:
E calculando a resultante no eixo :
Então, calculando o módulo desse vetor resultante, temos:
E sua direção será dada por:
Valeu, galera! Até a próxima! 😉