a. Suponha que o circuito da FIGURA P32.51 esteja aterrado no ponto d. Encontre o potencial em cada um dos quatro pontos a, b, c e d.
b. Desenhe o gráfico potencial versus posição, iniciando no ponto d e prosseguindo em sentido horário.
c. Repita os itens a e b para o mesmo circuito, agora aterrado no ponto a em vez de no ponto d
Passo 1
- Suponha uma bateria ideal e fios de conexão ideais.
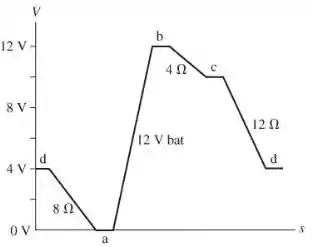
- Mover o terreno para o ponto a não altera a análise básica da parte (a) ou as diferenças de potencial encontradas lá. Tudo o que muda é que agora Va = 0 V. O ponto b é 12 V a mais que o ponto a por causa da bateria. Então, Vb = Va + 12 V = 12 V. O ponto c é 2 V menor que o ponto b, então Vc = Vb – 2 V = 10 V. O ponto d é 6 V menor que o ponto c, então Vd = Vc – 6 V = 4 V. O ponto a é 4 V menor que o ponto d, então Va = Vd – 4 V = 0 V. Isso nos traz de volta para onde começamos. As informações sobre os potenciais são mostradas no gráfico acima.
Aterrar um ponto não afeta a análise básica do circuito. Na Figura P32.51, há uma
loop único com uma única corrente I fluindo no sentido horário. Aplicando a lei das malhas de Kirchhoff no sentido horário
do canto inferior direito da
∑ΔV i = −8I + 12 V – 4I – 12I = 0 V ⇒
Conhecendo a corrente, podemos usar ΔV = IR para encontrar a diferença de potencial em cada resistor:
ΔV8 = 4 V ΔV4 = 2 V ΔV12 = 6 V
Passo 2
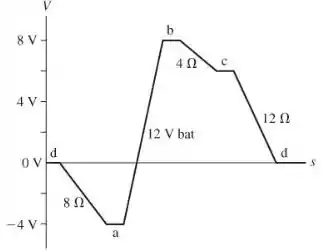
O objetivo de aterrar um ponto no circuito é estabelecer esse ponto como o potencial específico V = 0 V. O ponto de aterramento d, faz esse potencial = 0 V. Então podemos usar as diferenças de potencial conhecidas para encontrar o potencial em outros pontos do circuito. O ponto a é 4 V menor que o ponto d (porque o potencial diminui na direção de fluxo de corrente), então = – 4 V = – 4 V. O ponto b é 12 V a mais que o ponto a por causa da bateria. Então = + 12 V = 8 V. O ponto c é 2 V menor que ponto b, então = – 2 V = 6 V. O ponto d é 6 V menor que o ponto c, então = – 6 V = 0 V. Esta é uma consistência check - fazer um loop completo nos traz de volta ao potencial em que começamos, ou seja, 0 V
Passo 3
Resposta
Ver o desenvolvimento