
Passo 1
Podemos usar para expressar e expressa B em termos de e M.
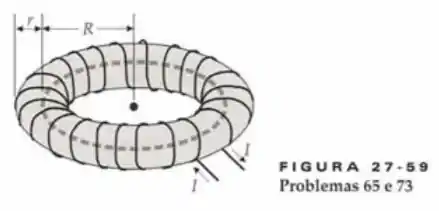
Vamos expressar dentro de uma toróide:
Passo 2
O campo B resultante no anel é a soma de e :


Podemos usar para expressar e expressa B em termos de e M.
Vamos expressar dentro de uma toróide:
O campo B resultante no anel é a soma de e :