Um tobogã desce uma colina e tem velocidade constante. O ângulo da colina é 8,00 em relação à horizontal. Qual é o coeficiente de atrito cinético entre a superfície da colina e o tobogã?

O tobogã tem velocidade constante, portanto, não tem aceleração e está em

equilíbrio. Portanto, as forças que atuam no tobogã devem se equilibrar, ou seja, a força resultante atuando no tobogã deve ser zero.

Existem três forças presentes, a força de atrito cinético (), a força normal da superfície inclinada () e o peso () do tobogã.

Usando a segunda lei de Newton com a aceleração igual a zero, obteremos o coeficiente do atrito cinético.

Ao desenhar o diagrama de corpo livre para o tobogã, o deve ser paralelo à superfície da colina e para baixo, a direção sendo perpendicular à superfície da colina. Nós também usamos para simbolizar a força de atrito.

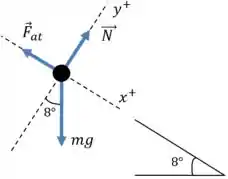
Uma vez que o tobogã está em equilíbrio, as forças resultantes em e são:

Na expressão para o equilíbrio em , podemos resolver para

E podemos substituir na primeira equação para o equilíbrio em