O desenho mostra um palhaço de circo que pesa 890 N. O coeficiente de atrito estático entre os pés do palhaço e o solo é 0,53. Ele puxa verticalmente para baixo uma corda que passa ao redor de três roldanas e é amarrada em torno de seus pés. Qual é o mínimo de força que o palhaço deve exercer para puxar seus pés fora de si mesmo?
Passo 1
Opaaa, tudo bem?
Vamos lá resolver mais uma questão muito interessante para nosso entendimento completo do capítulo!
A figura que o problema mostra é a seguinte

Passo 2
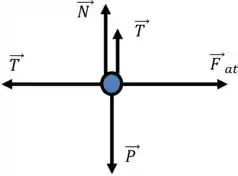
O diagrama de corpo livre no desenho abaixo mostra as forças que atuam sobre o palhaço (peso = ). Nesse desenho, observe que denota a força de tração. Já que a corda passa em torno de três polias, forças de magnitude são aplicadas nas mãos e nos pés do palhaço.
A força normal devido ao chão é , e a força de atrito estática máxima é . No instante antes de os pés do palhaço se moverem, a força resultante vertical e a resultante na horizontal são zero, de acordo com a segunda lei, uma vez que não há aceleração neste instante.
Passo 3
De acordo com a segunda lei de Newton, sendo direita e para cima sendo as direções positivas, temos
Da equação para a força horizontal nós achamos
Da equação para a força vertical nós achamos
Passo 4
Com as equações obtidas no passo anterior, podemos resolver para a força
Substituindo os valores dados: