Um trabalhador fica parado em um telhado inclinado em um ângulo de acima da horizontal. Ele está sendo impedido de escorregar por uma força de atrito estático de 390 N. Encontre a massa do trabalhador.
Passo 1
Oii tudo certo?
Vamos lá resolver mais uma questão muito interessante para nosso entendimento completo do capítulo!
Passo 2
O trabalhador está parado. Portanto, ele está em equilíbrio, e a força resultante atuando nele é zero.
A força de atrito estático que impede ele escorregue, aponta para cima ao longo do telhado, a um ângulo de graus acima da horizontal. Nós escolhemos como a direção (veja o diagrama de corpo livre).
A força normal é perpendicular ao telhado e, portanto, não tem componente .
A força gravitacional () da Terra sobre o trabalhador aponta diretamente para baixo e, portanto, tem um componente paralelo ao telhado.
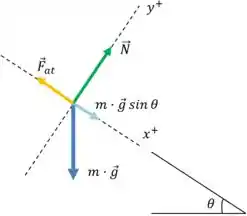
Usaremos este diagrama de corpo livre e encontraremos a massa do trabalhador aplicando a segunda lei de Newton, com a aceleração igual a zero.
Passo 3
A força de atrito aponta na direção , e a componente do peso do trabalhador () aponta na direção .
Já que não tem outras forças agindo na direção , e a aceleração do trabalhador é igual a zero, essas duas forças se equilibram.
A componente do peso do trabalhador é (), então
Passo 4
Resolvendo a equação obtida para a massa do trabalhador temos que: