Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.1 - Ex. 4
Três líquidos imiscíveis são despejados em um recipiente cilíndrico. Os volumes e massas específicas dos líquidos são : ; Qual é a força total exercida pelos líquidos sobre o fundo do recipiente? Um litro . (Ignore a contribuição da atmosfera).
Passo 1
Primeiro, considere , e as massas dos líquidos de volumes iguais a , respectivamente. Considere também como a força normal resultante da ação da pressão externa sobre o recipiente. Analisando as forças externas atuantes sobre o sistema, temos:
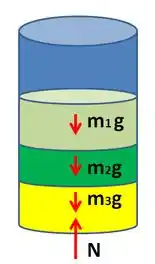
Do equilíbrio vertical de forças, temos que:
Passo 2
Sendo assim, a força total exercida pelos três líquidos sobre o fundo do recipiente é igual à força , tal que:
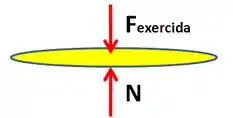
Assim, temos que, sendo e as massas específicas de cada líquido:
Logo:
Resposta
Exercícios de Livros Relacionados
A Equação 14.7 mostra que uma razão de 100 para 1 pode fornecer uma força na saída 100 vezes maior que a força na entrada. Isso não viola a conservação da energia? Explique.
Comparando os exemplos 14.1 (Seção 14.1) e 14.2 (Seção 14.2), parece que um peso de 700 N de ar exerce uma força para baixo igual a 2,0 × 10 6N sobre o piso. Como isso é possível?
Suponha que a porta de uma sala esteja ajustada ao batente sem atrito, impedindo a passagem do ar. Se a pressão de um lado da porta for igual a uma atmosfera-padrão e a pressão do outro lado for 1 % m
A uma certa profundidade em um líquido incompressível, a pressão absoluta é P . A uma profundidade duas vezes maior, a pressão absoluta será igual, maior ou menor que 2 P ? Justifique sua resposta.
Quando uma corrente de água sai suavemente de uma torneira, sua largura diminui à medida que a água cai. Explique por que isso acontece.