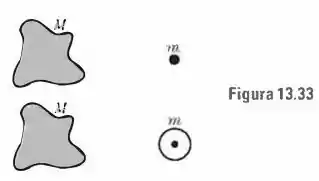
Utilizando os resultados da Seç. , prove que a interação gravitacional entre uma massa de forma arbitrária (Fig. ) e uma massa puntiforme é igual à interação entre e um corpo esférico homogêneo de massa , desde que o centro do corpo esférico coincida com a posição da massa puntiforme.

E aí, beleza?? Pela terceira lei de Newton, a força que exerce em é a mesma que exerce em . Portanto, vamos estudar a força que faz em . Note que essa força é dada pela integral:

Assim, a força depende diretamente do campo gravitacional ao qual está submetido. Entretanto, o campo gravitacional gerado pela massa pontual e a esfera de massa são idênticos (desde que a massa pontual seja colocada no ponto exato correspondente ao centro da esfera). Ou seja, a integral da força que exerce em dará o mesmo resultado.

Assim, pela terceira lei de Newton, podemos garantir que a interação gravitacional entre uma massa de forma arbitrária e uma massa puntiforme é igual à interação entre e um corpo esférico homogêneo de massa , desde que o centro do corpo esférico coincida com a posição da massa puntiforme.