Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Oscilações, Ondas e Termodinâmica- Ed: 5º - Capítulo 13.Problemas - Ex. 57
Um vaso é derrubado do parapeito da janela de uma altura d = 20,0 m acima da calçada, como mostrado na Figura P13.57. Ele vai em direção a um homem de altura h = 1,75 m que está em pé embaixo. Suponha que o homem necessite de um intervalo de tempo ∆t = 0,300 s para responder à advertência. Quão perto da calçada o vaso pode cair antes que seja tarde demais para um grito de aviso, a partir do parapeito, chegar a tempo ao homem?
Passo 1
Faaaaaalaaa galera, show de bolaa??
Arrasta pra cima e só vamoo!!
A situação do enunciado pode ser observada no esquema seguinte. Apesar de tudo ocorre em uma mesma linha vertical, representamos cada instante ao lado do outro para conseguimos uma melhor visualização a cada etapa do problema.
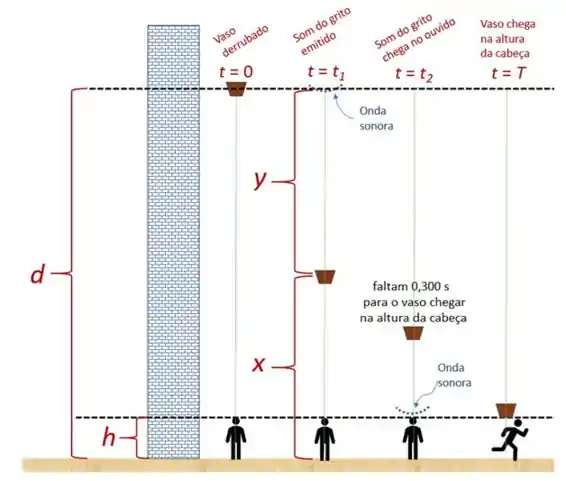
Com base na figura acima, a pergunta do enunciado pode ser colocada como : qual e o valor de x?
Passo 2
Partindo da cinética, vamos relembrar da relação entre altura de queda e o tempo de queda:
Primeiramente, iremos calcular o ;
Cálculo de ;
Passo 3
Tá, mas como posso calcular o ??
Opaaa vem comigooo
Basta perceber que, entre , o som percorreu a distância , portanto:
Cálculo de y:
Passo 4
Portanto, por meio do seguinte cálculo de x podemos afirmar que o vaso pode cair de modo seguro:
Resposta
Portanto, o vaso pode cair de modo seguro à 7,83m.