Para medir sua velocidade, um paraquedista carrega um alarme que emite um som constante de 1.800 Hz. Um amigo no local do pouso, diretamente abaixo, escuta o som amplificado. Suponha que o ar esteja calmo e que a velocidade do som seja independente da altitude. Enquanto o paraquedista está caindo a uma velocidade terminal, seu amigo no chão recebe ondas de frequência de 2.150 Hz. (a) Qual é a velocidade de descida do paraquedista? (b) E se? Suponha que o paraquedista possa ouvir o som da buzina refletida no chão. Qual a frequência que ele recebe?
Passo 1
Faaaaaalaaa galera, show de bolaa??
Arrasta pra cima e só vamoo!!
- A situação do item (a) está representada na figura a seguir:
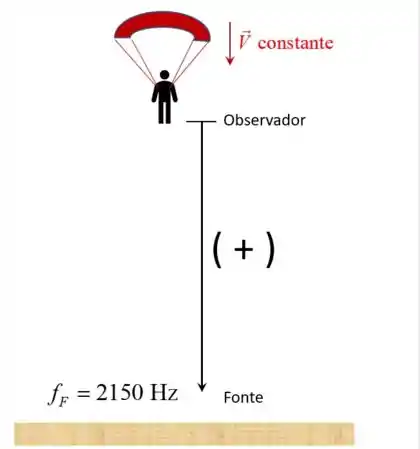
- A situação do item b está representada na figura a seguir. Agora o som refletido no chão é o sim da fonte, ou seja: , e o sentido da equação é para baixo, e a velocidade da fonte (solo) é nula:
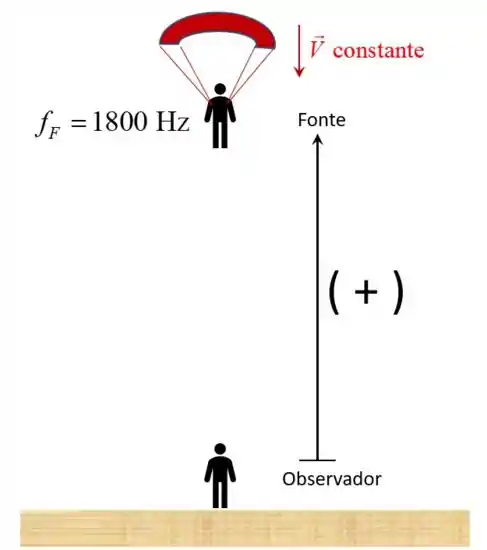
Na equação do efeito Doppler, o sentido de sinal positivo será para cima, já que é este o sentido: observador/a para a fonte. Além do mais, a velocidade do/a observador/a é nula, pois ela/e está parado/a no solo. Assim, temos:
Passo 2
Assim iremos obter: