Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 8.Problemas - Ex. 19

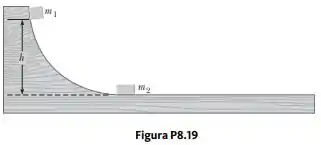
Dois blocos estão livres para deslizar ao longo da pista de madeira sem atrito mostrada na Figura P8.19. O bloco de massa m 1   =   5,00   k g é solto da posição mostrada, a uma altura h   =   5,00   m acima da parte plana da pista. Saindo de sua extremidade frontal está o polo norte de um ímã forte, que repele o polo norte de um ímã idêntico embutido na extremidade posterior do bloco de massa m 2   =   10,0   k g inicialmente em repouso. Os dois blocos nunca se tocam. Calcule a altura máxima até a qual m 1 sobe após a colisão elástica.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

A energia mecânica do sistema isolado bloco-Terra é conservada à medida que o bloco de massa m 1 desliza na pista. Primeiro, encontramos v 1 , a velocidade de m 1 quando ele chega à posição horizontal antes da colisão:

K i + U i = K f + U f 1 2 m 1 v 1 2 + 0 = 0 + m 1 g h v 1 = 2 9.80 m s 2 5.00 m = 9.90 m / s

Agora, antes da colisão:

v 1 f = m 1 - m 2 m 1 + m 2 v 1 = - 1 3 9.90 m s = - 3.30 m s

Passo 2

Agora, o bloco de 5kg volta ao seu ponto mais alto após a colisão de acordo com:

m 1 g h m a x = 1 2 m 1 ( - 3.30 m / s ) 2

h m a x = ( - 3.30 m / s ) 2 2 9.80 m s 2 = 0.556 m

Resposta

0.556 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um próton, que se move na velocidade v ii ^ , colide elasticamente com outro que está inicialmente em repouso. Supondo que ambos tenham velocidades iguais após a colisão, encontre (a) a velocidade de
Dois discos de shuffleboard de massas iguais, um laranja e outro amarelo, estão envolvidos em uma colisão oblíqua elástica. O disco amarelo está inicialmente em repouso e é atingido pelo disco laranja
Uma bola de bilhar movendo-se a 5,00m / s colide com outra parada com a mesma massa. Após a colisão, a primeira bola se move a 4,33m / s a um ângulo de 30,0 ° em relação à linha original de movimento.
Conforme mostra a Figura P8.20, uma bala de massa m e de velocidade escalar v passa completamente pelo pêndulo de massa M . A bala surge com uma velocidade dev / 2 . O pêndulo é suspenso por uma haste