Deformação em estruturas hiperestáticas – verificação do diagrama com carregamento externo
Produzido por Pablo RicardoTeoria
Introdução
Suponha que o professor de antemão já forneça pra gente o diagrama da estrutura hiperestática, por exemplo, com o carregamento externo. Com esse diagrama seria possível determinar as deformações da nossa estrutura? Perceba que seria um processo contrário ao que aprendemos.
O que vimos até aqui era a maneira de, a partir das deformações, chegar nos diagramas. Agora o nosso objetivo vai ser aprender como que a partir dos diagramas podemos chegar nas deformações.
Para isso vamos ver que precisamos tomar uma decisão. Essa decisão vai ter duas formas de ser tomada, e vamos ver aqui em baixo como devemos fazer isso.
Caso 1 – carregamento externo na estrutura hiperestática
Como sabemos, sempre que resolvemos uma estrutura hiperestática, nós quebramos ela até termos uma estrutura do tipo isostática. E com isso passamos a ter duas estruturas. E o que fazemos com ela? Vamos fazer um exemplo.
Suponha que queremos saber a deformação vertical no centro da seguinte viga.
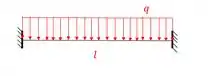
Então sabemos que a nossa estrutura hiperestática é.
![]()
E como eu disse, toda estrutura hiperestática podemos quebrar vínculos até obtermos a estrutura isostática, que nesse caso podemos ter como exemplo a seguinte estrutura:
![]()
E agora como eu disse precisamos fazer uma escolha. Em uma estrutura vamos por o carregamento externo, e vamos ter o seu diagrama. Enquanto que na outra, vamos por o carregamento unitário, na direção e sentido que desejamos saber o deslocamento, e vamos obter também o diagrama.
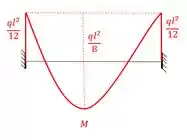
Como já sabemos, no nosso primeiro caso vamos por o carregamento principal na estrutura hiperestática, tendo assim a seguinte estrutura:
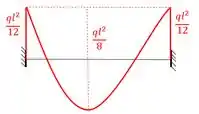
E com isso obtemos o seguinte diagrama de momentos fletores.
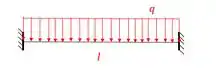
Logo, se escolhemos a estrutura hiperestática para receber o carregamento externo, vai ser na estrutura isostática que vamos pôr o carregamento unitário.
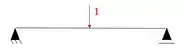
E o diagrama será:
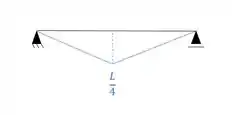
E agora você pode se perguntar, e daí que eu tenho os diagramas?
É aqui que iremos usar a nossa formulazinha, relembrando o nosso princípio dos trabalhos virtuais, vamos ter que:
Em que:
Que no nosso exemplo será o seguinte diagrama:
Da mesma maneira teremos que:
Que no nosso caso é o seguinte diagrama:
Seguindo os dados do nosso exemplo podemos ver que não vamos analisar cortante, nem normal e nem torsor, então podemos de cara descartar esses termos na nossa fórmula, e sobra apenas:
E como podemos supor constante por toda a estrutura, podemos escrever a nossa fórmula como:
E perceba que nada mais é que combinarmos os nossos diagramas como já fazíamos antes. O jeito mais fácil de fazer essa combinação de diagramas é pelo Método das Tabelas, usando as fórmulas da tabela de Kurt Beyer.
A parada é que na tabela de Kurt Beyer só tem alguns formatos de diagramas e não tem essa parábola deslocada pra cima da viga biengastada (esse deslocamento aparece justamente porque a viga é biengastada, porque se fosse biapoiada, o momento seria nulo nos apoios... mas isso é só uma curiosidade). Nós vamos então decompor o primeiro diagrama em 2 partes: uma parábola e um retângulo.
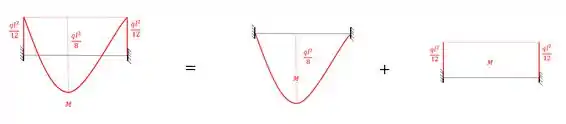
Agora, em vez de combinar o diagrama da estrutura hiperestática com o da estrutura isostática, vamos combinar as duas partes do primeiro com o segundo. Confuso? Olha esse esquema.

Temos que fazer 2 combinações de diagramas e somar as expressões:
Cuidado com os sinais! A primeira combinação fica positiva porque os 2 diagramas estão pra baixo (se os 2 estiverem pra cima também fica positivo) e a segunda fica negativa, porque um está pra baixo e o outro pra cima.
E assim determinamos o deslocamento no centro da nossa viga a partir dos diagramas, considerando o carregamento principal na estrutura hiperestática:
Caso 2 – carregamento externo na estrutura isostática
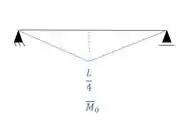
Vamos supor exatamente o mesmo exemplo, mas agora vamos trocar a posição dos carregamentos, ou seja, vamos supor o carregamento principal na estrutura isostática, e o carregamento unitário na hiperestática, e vamos ver o que teremos de diagramas:
- Carregamento externo na estrutura isostática:
- Carregamento unitário na estrutura hiperestática:
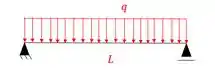
Que gera o seguinte diagrama:
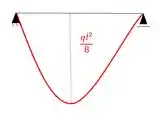
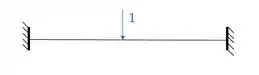
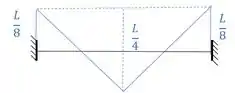
Que gera o seguinte diagrama:
É aqui que iremos usar a nossa formulazinha, relembrando o nosso princípio dos trabalhos virtuais, porém tomando cuidado, porque a nossa fórmula sofre uma pequena mudança que será:
Em que:
Que no nosso exemplo será o seguinte diagrama:
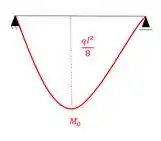
Da mesma maneira teremos que:
Que no nosso caso é o seguinte diagrama:
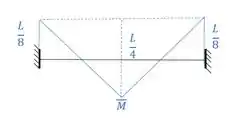
Seguindo os dados do nosso exemplo podemos ver que não vamos analisar cortante, nem normal e nem torsor, então podemos de cara descartar esses termos na nossa fórmula, e sobra apenas:
E como podemos supor constante por toda a estrutura, podemos escrever a nossa fórmula como:
E perceba que nada mais é que combinarmos os nossos diagramas como já fazíamos antes.
Do mesmo jeito que aconteceu no caso anterior, o diagrama da viga biengastada está deslocado pra cima. Então vamos decompor esse formato triangular deslocado em um triângulo simples e um retângulo.

Agora vamos combinar essas 2 partes com o diagrama da estrutura isostática. Novamente um termo vai ser positivo e outro negativo.

E perceba que mesmo com o segundo caso chegamos exatamente no mesmo valor de deslocamento vertical. Ou seja, podemos escolher tanto o caso 1, e a fórmula 1, quanto o caso 2 com a fórmula 2 para obtermos os deslocamentos na estrutura hiperestática a partir dos seus diagramas. Agora bora fazer exercício pra deixar tudo isso muito bem encaminhado e assim podermos ficar tranquilo na hora de fazer esse tipo de exercício.