Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 14a
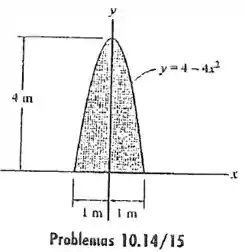
10.14 Determine o momento de inércia da área em relação ao eixo . Resolva o problema de duas maneiras, usando elementos diferenciais retangulares: (a) com uma espessura de e (b) com uma espessura de .
Passo 1
a.
Fala! Nós precisamos escolher um elemento infinitesimal de área que seja paralelo ao eixo , assim ele tem largura como o enunciado pede e altura , como vemos na figura:
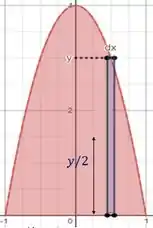
Os pontos desse elemento de área não se encontram à mesma distância do eixo então vamos precisar do teorema dos eixos paralelos para cada elemento de área.
A gente sabe que o momento de inercia de um retângulo, em relação ao eixo do seu centroide, é igual a
A base do retângulo é , sua altura é . Então o momento de inercia no centroide do retângulo é
Pelo teorema dos eixos paralelos:
Onde é a coordenada do centroide do elemento de área, que vale e é igual a , área do elemento. Então:
Sabemos que , logo
Passo 2
Então, a fórmula para calcularmos o momento de inercia total, vai ficar:
Nós vamos integrar de a , porque esse é o intervalo de :
Vamos tirar a constante para fora da integral:
Integral de polinomia fica facinho de resolver:
A equação ficou gigante, mas é só fazer com calma e cuidar pra não errar nada: