3.31. As molas no arranjo de cabos estão originalmente deformadas em quando . Determine a força vertical que deve ser aplicada, de modo que .
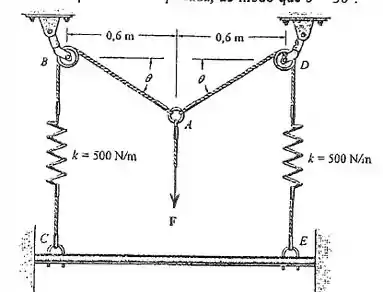
Passo 1
Fala, querido! Queremos determinar , para que .
Vamos começar analisando a distância da corda que está entre B e A, e consequentemente D e A (porque nosso problema é simétrico, tudo que acontece na direita acontece na esquerda).
De acordo com o triângulo
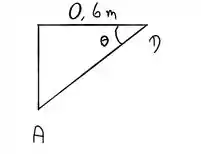
Podemos tirar que então podemos concluir que
Vamos fazer o DCL de A, onde é aplicada, que não pode faltar
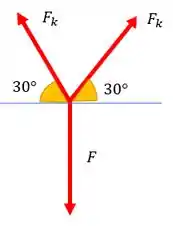
Agora podemos usar a equação de equilíbrio para determinar as forças.
Passo 2
Vamos determinar as forças em BA e AD que serão as mesmas, repare na simetria do problema, vamos chamar de .
Esse é o deslocamento da mola, quando temos. Vamos refletir um pouco.
Quando a gente tinha , o deslocamento era . Mas como a gente puxou essa corda, a mola teve que se esticar para que os segmentos ED e BC permanecem com os tamanhos originais.
Então para achar esse valor que esticou vamos achar o comprimento da corda da direita em e subtrair pelo comprimento em .
- em :
- em :
Como a mola já estava deformada de 0,3 no início, a deformação total é:
Então
Passo 3
Agora vamos usar as condições de equilíbrio para o eixo y
Então