Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 10.Problemas fundamentais - Ex. 2

10.2 Determine o momento de inércia da área sombreada em relação ao eixo x .

Passo 1

Fala ai galerinha do RespondeAí, tudo beleza?

Saca só, o enunciado nos deu uma região no plano dividida pela função y 3 = x 2 e pediu pra gente encontrar o momento de inércia dessa área em relação ao eixo x . Pra isso a gente pode lembrar da fórmula do momento de inércia em relação ao eixo x :

I x = ∫ A   y 2 d A

Então a malandragem agora é a gente escolher um elemento infinitesimal de área que seja paralelo ao eixo x :

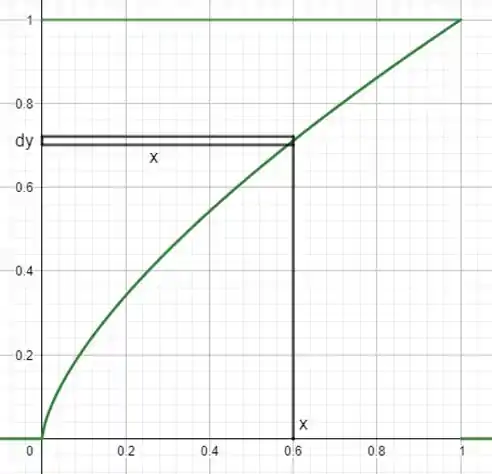
Isso quer dizer que esse elemento infinitesimal d y vai gerar uma área infinitesimal d A se a gente multiplicar ele por x :

Segue que o elemento infinitesimal de área vai ser igual a:

d A = x d y

Isolando x na função dada, vamos ter que:

y 3 = x 2

x = y 3 / 2

Então substituindo no nosso elemento de área:

d A = y 3 / 2 d y

Passo 2

Shwo de bolinhas, agora a gente pode juntar tudo na nossa integral do momento em relação a x :

I x = ∫ A y 2 d A

Como y vai de 0 até 1 , teremos que:

I x = ∫ 0 1 y 2 y 3 / 2 d y

I x = ∫ 0 1 y 7 / 2 d y

Resolvendo a integral:

I x = y 9 / 2 9 / 2 0 1

I x = 1 9 / 2 9 2

I x = 2 9

Portanto, o momento em relação ao eixo x será:

I x = 0,222   m 4  

Resposta

I x = 0,222   m 4  

Ver Outros Exercícios desse livro