Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 57
Determine a intensidade da força , de modo que a força resultante das três forças seja a menor possível. Qual é a intensidade dessa força resultante mínima?
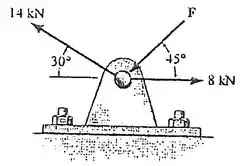
Passo 1
Queremos a intensidade e a direção da força resultante, sabemos que:
Vamos começar pelas componentes em , sabemos que tem o , mas vamos deixá-lo pro final:
Nossas componentes em :
E nossa força resultante fica:
Passo 2
Nossa força resultante está em função de , como queremos um ponto de mínimo se derivarmos dos dois lados e igualarmos a 0 descobriremos no ponto de mínimo:
Igualando a 0, não se preocupa com o porque ele zera também:
E então:
Passo 3
Finalmente, usando a equação do módulo:
Resposta
Exercícios de Livros Relacionados
A intensidade da força F é 400N . Expresse F como um vetor, em termos dos vetores unitários i e j . Identifique componentes escalares e vetoriais de F .
A força F tem intensidade de 600N . Expresse F como um vetor, em termos dos vetores unitários i e j . Identifique os componentes escalares de F em x e y .
O controle da haste A P exerce uma força F sobre o setor circular, como mostrado. Determine os componentes de força em x - y e n - t .
Determine as componentes n e t da força F que a haste A B exerce sobre a manivela A O . Avalie sua expressão geral para F = 100N e (a) θ = 30 ° , β = 10 ° e (b) θ = 15 ° , β = 25 ° .