Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 22
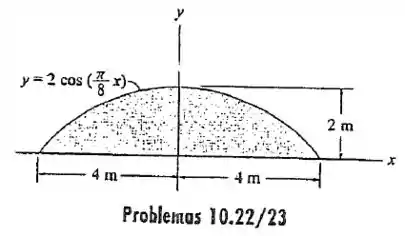
10.22 Determine o momento de inércia da área em relação ao eixo .
Passo 1
A fórmula do momento de inércia em relação ao eixo é
Mas se a gente tentar pegar um elemento infinitesimal de área paralelo ao eixo , vamos ter que isolar o para deixar tudo em função de e calcular aquela integral. E ai vamos ter um problemão, porque o tá dentro do cosseno e não vamos conseguir isolar ele.
Por isso, vamos escolher um elemento infinitesimal de área, que seja paralelo ao eixo :
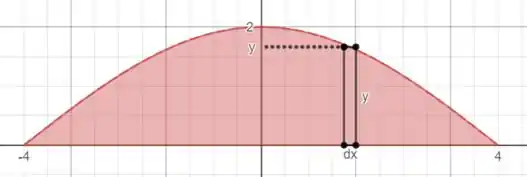
Os pontos desse elemento de área não se encontram à mesma distância do eixo então vamos precisar o teorema dos eixos paralelos para cada elemento de área. A gente sabe que o momento de inercia de um retângulo, em relação ao eixo do seu centroide, é igual a
A base do retângulo é , sua altura é . Então o momento de inercia no centroide do retângulo é
Pelo teorema dos eixos paralelos:
Onde é a coordenada do centroide do elemento de área, que vale e é igual a . Então:
Sabemos que , logo
Passo 2
Então, a fórmula para calcularmos o momento de inercia total, vai ficar:
Nós vamos integrar de a :
Aqui vamos ter que lembrar de umas coisinhas de Cálculo 1
Passo 3
Primeiro vamos usar substituição:
Os limites de integração vão ficar assim:
Para
E para
A integral vai ficar dessa forma:
Tirando a constante para fora da integral
Passo 4
Vamos separar o cosseno ao cubo dessa forma:
Sabemos pelas relações trigonométricas que
Substituindo isso na integral
Agora, nós vamos usar substituição mais uma vez. Se falarmos que
Então
e
Os limites de integração vão ficar
Para
E para
A equação vai ficar:
Passo 5
Agora é uma integral simples de resolver