Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 15b

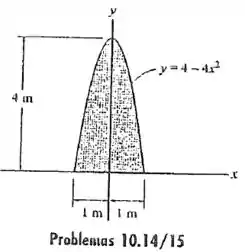
10.15 Determine o momento de inércia da área em relação ao eixo y . Resolva o problema de duas maneiras, usando elementos diferenciais retangulares: (a) com uma espessura de d x e (b) com uma espessura de d y .

Passo 1

Belezoca galerinha, agora aqui na letra (b), vamos precisar fazer um pouquinho diferente da letra (a), saca só, nós precisamos escolher um elemento infinitesimal de área que seja paralelo ao eixo x :

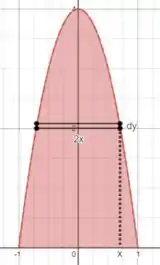
A gente sabe que o momento de inercia de um retângulo, em relação ao eixo y do seu centroide, é igual a:

I = 1 12 ⋅ h b 3

Além disso, também sabemos que o momento de inércia da área em relação a y será:

I y = ∫ d I y

Como a base do retângulo é 2 x e sua altura é d y . Então o momento de inercia no centroide do retângulo será:

d I y = 1 12 ⋅ d y ⋅ 2 x 3

d I y = 8 x 3 12 d y

d I y = 2 x 3 3 d y

Isolando x na função do gráfico, vamos obter que:

y = 4 - 4 x 2

4 x 2 = 4 - y

x 2 = 4 - y 4

Logo:

x = 4 - y 4

x = 4 - y 2

Substituindo no diferencial do momento de inercia:

d I y = 2 x 3 3 d y

d I y = 2 3 4 - y 2 3 d y

d I y = 1 12 4 - y 3 d y

Passo 2

Iradoso, agora se a gente substituir os termos que a gente encontrou na fórmula do momento de inércia no eixo y , vamo obter que:

I y = ∫ d I y

I y = ∫ 0 4 1 12 4 - y 3 d y

I y = 1 12 ∫ 0 4 4 - y 3 d y

Agora pra gente resolver essa integral ai de dentro, podemos usar a técnica de substituição:

u = 4 - y ,     d y = - d u

De modo que nossa integra se torna:

I y = 1 12 ∫ 0 4 u 3 d u

Sendo assim, obtemos:

I y = 1 12 ∫ 0 4 u 3 / 2 d u

I y = 1 12 2 u 5 / 2 5 0 4

I y = 1 12 2 4 5 / 2 5

Portanto:

I y = 1,07   m 4

Resposta

I y = 1,07   m 4

Ver Outros Exercícios desse livro