Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 10.Problemas - Ex. 38
10.34 Determine a distância até o centroide da área da seção transversal da viga; depois, determine o momento de inércia em relação ao eixo .
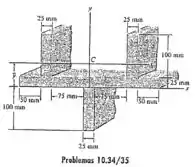
Passo 1
Faaala galerinha do RespodenAí, tudo beleza???
Saca só, esse exercício aqui começa pedindo pra gente calcular a distância , até o centroide da figura composta. Sabemos que a fórmula para de uma figura composta é dada como:
E sabendo disso, o enunciado também quer que a gente encontre o momento de inércia da seção transversal em relação ao eixo que passa pelo centroide da figura.
Belezoca, o macete pra gente começar a questão, é separar essa área em 4 retângulos, desse jeito:
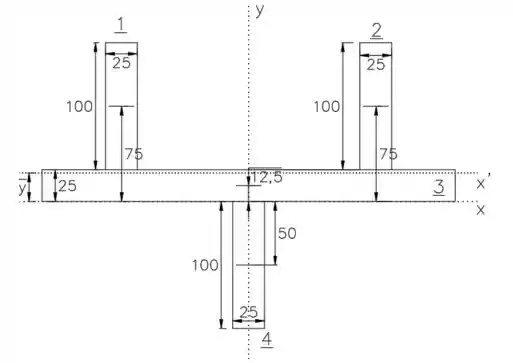
Agora com as figuras separadas, podemos calcular o que o enunciado pede pra gente.
Passo 2
Iradoso, agora podemos montar uma tabelinha com as posições de cada figura:
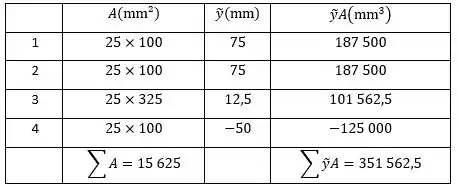
Sendo assim, a posição será:
Belezera, agora é só a gente calcular o momento de inercia.
Passo 3
O centroide dos retângulos não coincide com o eixo que estamos usando para calcular o momento de inercia, então precisamos usar o teorema dos eixos paralelos. Vamos calcular o momento de inercia de cada retângulo e depois soma-los.
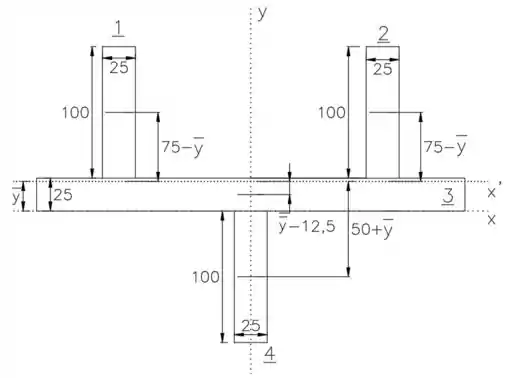
Pela tabela sabemos que o momento de inercia de um retângulo é igual a , usando o teorema dos eixos paralelos vamos ter que:
Os retângulo 1 e 2 terão o mesmo momento de inercia, pois tem as mesmas medidas e a mesma distância até o eixo . Logo, os momentos de inercia vão ficar assim:
Retângulos 1 e 2:
Retângulo 3:
Retângulo 4:
Para descobrirmos o momento de inercia total, só precisamos somar os momentos de inercia de cada retângulo, de modo que:
Portanto: