Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 40

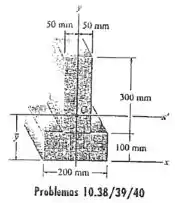
10.40 Determine o momento de inércia da área da seção transversal em relação ao eixo y .

Passo 1

Cara, vamos lá! Ele quer o momento de inércia dessa seção em relação a y .

Percebe que y é um eixo de simetria da seção, então a gente não vai precisar usar o teorema dos eixos paralelos aqui, bele?

Agora repara que essa seção pode ser entendida como dois retângulos. Um seção composta.

Vamos separar essa área assim:

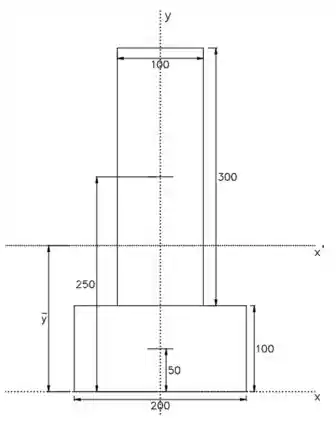
O momento de inércia total será a soma dos momentos de inercia desses dois retângulos:

I y = I y _ s u p e r i o r   + I y _ i n f e r i o r

Passo 2

Pela tabela, sabemos que o momento de inércia de um retângulo, em relação ao eixo y , é igual a 1 12 h b 3 .

Sendo que h é o comprimento do segmento paralelo a y .

Para o retângulo superior teremos que h = 300 e b = 100 :

1 12 h b 3 s u p e r i o r = 1 12 300 100 3

E para o retângulo inferior, o segmento paralelo a y vale h = 100 , logo b = 200 e:

1 12 100 200 3 i n f e r i o r = 1 12 100 200 3

Passo 3

Nosso momento de inércia de toda a área fica:

I y = 1 12 h b 3 s u p e r i o r + 1 12 h b 3 i n f e r i o r

I y = 1 12 300 100 3 s u p e r i o r + 1 12 100 200 3 i n f e r i o r

I y = 91,7 ⋅ 10 6   m m 4

Para passar para metros, a gente multiplica por

10 - 3 4 = 10 - 12

Já que temos 4 dimensões de m m , e para passar isso para metro multiplicamos por 10 - 3 . Aí temos:

I y = 91,7 ⋅ 10 6 ⋅ 10 - 12 = 91,7 ⋅ 10 - 6 = 9,17 ⋅ 10 - 5   m 4

Resposta

I y = 9,17 ⋅ 10 - 5   m 4

Ver Outros Exercícios desse livro