Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 52
10.52 Determine o momento de inércia da viga em relação ao eixo centroidal .
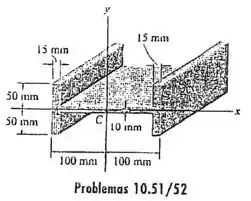
Passo 1
Fala ai galerinha do RespondeAí, tudo beleza?
Saca só, o macete nesse exercício aqui é a gente dividir essa área em 3 retângulos:
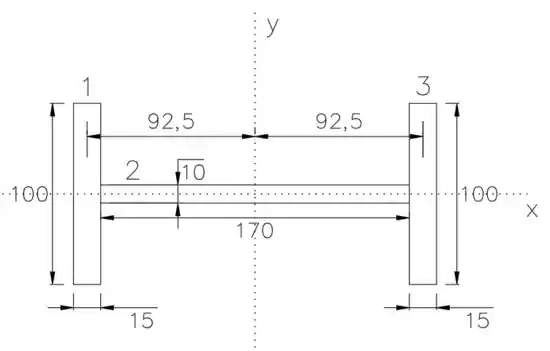
O momento de inercia para o eixo será a soma do momento de inercia dos três retângulos.
Passo 2
Iradoso, agora o momento de inercia de um retângulo, em relação ao eixo , é igual a . Como o centroide do retângulo do meio passa pelo eixo , não será necessário usar o teorema dos eixos paralelos para esse retângulo, já para os outros dois sim, então:
Precisamos da área dos retângulos que estão nos lados, assim como a distâncias de seus centroides até o eixo .
A distância do centroide até o eixo também é igual para os dois retângulos:
A equação va ficar assim: