Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 10.Problemas fundamentais - Ex. 7
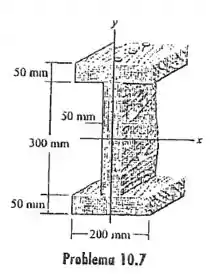
10.7 Determine o momento de inércia da área da seção transversal do canal em relação ao eixo .
Passo 1
Falaaa! A gente quer o momento de inércia em relação ao eixo . Essa seção é diferentona, mas a gente pode dividir em figuras mais simples para calcular o momento de inércia.
Vamos dividir essa área em 3 retângulos:
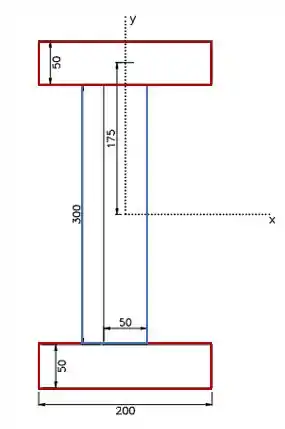
O momento de inércia total será a soma dos momentos de inercia desses três retângulos:
Repara que temos 2 retângulos iguais, esses em vermelho. Além de eles terem seus tamanhos iguais a distância de seus centroides até o eixo é igual, por essa razão, só precisamos calcular o momento de inércia de um e multiplicar o resultado por 2.
Ficamos assim:
Passo 2
Pela tabela, sabemos que o momento de inércia de um retângulo, em relação ao eixo , é igual a , onde é a dimensão do segmento do retângulo paralelo a , então nossa equação vai ficar:
O centroide desses retângulos coincide com o eixo , por isso não precisamos do teorema dos eixos paralelos para eles. Vamos listar nossos dados. A gente os acha olhando a figura
Como temos o tamanho das bases e das alturas desses retângulos só precisamos substituir na equação: