Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 136
136. Um pedaço de chapa metálica de de espessura é cortado e dobrado para formar o componente de máquina mostrado na figura. Sabendo que a massa específica do aço é , determine o momento de inércia de massa do componente em relação a cada um dos eixos de coordenadas.
Passo 1
Para determinar o momento em relação a cada eixo, vamos separar nossa figura em três partes, da seguinte forma:
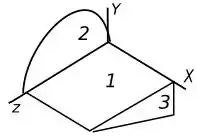
Assim o momento em relação a cada eixo é a soma dos momentos dessas três partes em relação ao eixo que estivermos trabalhando.
Só que para calcular os momentos de inercia das três partes, teremos que usar o teorema dos eixos paralelos já que o cálculo é em relação ao eixos coordenados mostrados na figura e só sabemos com facilidade o momento de inércia dessas peças quando os eixos coordenados estão alinhados com a figura de interesse que é fornecido pela figura do livro.
O teorema dos eixos paralelos é seguinte:
Onde é o momento que já conhecemos, é massa do objeto que estamos calculando e é a distância entre os dois eixos paralelos, que estão sendo considerados para determinar o momento de inércia.
Segundo a figura o momento de inercia, para a parte em relação aos eixos coordenados que estão alinhados a ela é:
Para parte temos:
Para parte temos:
Lembrando que não temos os mesmos e para isso é só para representar a fórmula, os valores dessas letras acharemos pela figura, assim como o não é igual.
Então vamos precisar da massa de cada parte, mas a massa de um objeto é dada por:
Onde é a massa específica do material e o volume do objeto.
Passo 2
Vamos calcular as massas para os nossos objetos.
Para :
Para :
Passo 3
Agora vamos começar calculando o momento em relação ao eixo , então:
Aplicando o teorema dos eixos paralelos.
Nossa, que contas chatas de se fazer, mas não tem como fugir, continuando.
Passo 4
Agora vamos calcular o momento em relação ao eixo , então:
Aplicando o teorema dos eixos paralelos.
Nossa, que contas chatas de se fazer, mas não tem como fugir, continuando.
Passo 5
Agora vamos calcular o momento em relação ao eixo , então:
Aplicando o teorema dos eixos paralelos.
Nossa, que contas chatas de se fazer, mas não tem como fugir, continuando.