Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 19

19- Determine o momento de inércia e o raio de giração da superfície sombreada mostrada na figura em relação ao eixo x .

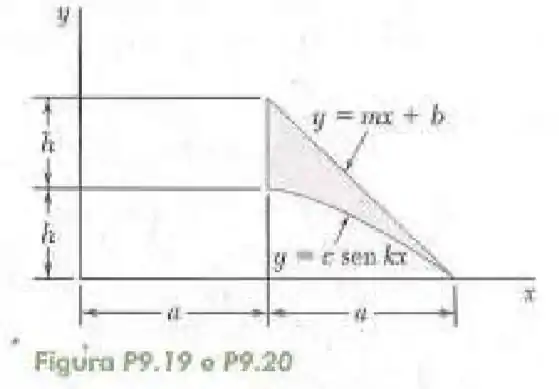
Passo 1

Vamos encontrar o elemento de área por linhas verticais tal como na figura abaixo.

Onde y r é o y da reta e y s é o y da função seno. Porém antes vamos aplicar os pontos ( a , 2 h ) e ( 2 a , 0 ) para encontrar as constantes da equação da reta e os pontos ( a , h ) e ( 2 a , 0 ) para encontrar as constantes na função seno.

Começando pela equação da reta:

a , 2 h → 2 h = m a + b

2 a , 0 → 0 = 2 a m + b

Pela segunda equação nós podemos tirar:

m = - b 2 a

Aplicando isso na primeira vemos:

2 h = - b 2 a   a + b

2 h = - b 2 + b = b 2

b = 4 h

Logo a equação da reta será:

y = - 4 h 2 a x + 4 h = - 2 h a x + 4 h

Agora para encontrar as constantes na função seno nós temos:

a , h → h = c sin ⁡ a k

2 a , 0 → 0 = c   s e n   2 a k

Na segunda equação nós podemos escrever que:

s e n   2 a k = 0

Com isso nós podemos dizer que:

2 a k = 0 ± π c

Se considerarmos c = + 1 nós teremos:

k = π 2 a

Agora aplicando esse resultado na primeira equação nós podemos dizer que:

h = c   s e n a π 2 a

h = c

Logo a equação senoidal será:

y = h   s e n π x 2 a

Então o elemento de área d A será igual a:

d A = - 2 h a x + 4 h - h   s e n π x 2 a d x

Passo 2

A área então para essa superfície será igual a (vendo que x varia de a até 2 a ) :

A = ∫ a 2 a - 2 h a x + 4 h - h   s e n π x 2 a d x

A = - h x 2 a a 2 a + 4 h x a 2 a + h c o s   π x 2 a × 2 a π a 2 a

Aplicando o intervalo:

A = - 4 a 2 h a + a 2 h a + 8 a h - 4 a h + 2 a h π - 1 - 0

A = - 3 a h + 4 a h - 2 π a h = 1 - 2 π a h  

Passo 3

Porém sabendo que estamos querendo encontrar a inércia em x fazendo por linhas verticais, isso nos daria o seguinte elemento de inércia:

d I x = 1 3 y 3   d x = 1 3 y r 3 - y s 3 d x

Pois é como se fosse a diferença entre a inércia da curva superior com a inferior.

Integrando as duas funções nós temos:

I x = 1 3 ∫ a 2 a - 2 h a x + 4 h 3 + h   s e n π x 2 a 3 d x

I x = h 3 3 ∫ a 2 a - 2 + 4 a a 3 + s e n 3 π x 2 a d x

Abrindo esse polinômio e fazendo:

sin 3 ⁡ θ = sin ⁡ θ sin 2 ⁡ θ = sin ⁡ θ 1 - cos 2 ⁡ θ = sin ⁡ θ - sin ⁡ θ cos 2 ⁡ θ

Nós encontramos:

I x = 2 a h 3 3 + 4 a h 3 9 π

I x = 2 a h 3 3 1 - 2 3 π

Passo 4

Dessa forma o raio de giro em x será igual a:

k = I x A

k = 2 a h 3 3 1 - 2 3 π 1 - 2 π a h

k = h 2 3 1 - 2 3 π 1 - 2 π

Em números isso será:

k = 1.202   h

Resposta

I x = 2 a h 3 3 1 - 2 3 π

k = 1 . 202   h

Ver Outros Exercícios desse livro