Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 15

15- Determine o momento de inércia e o raio de giração da superfície sombreada mostrada na figura em relação ao eixo x .

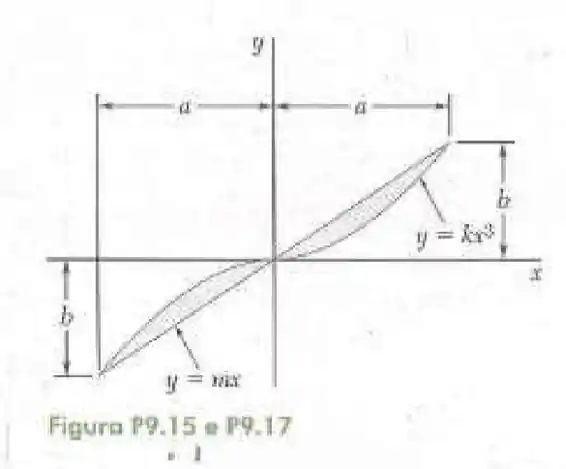
Passo 1

Aplicando o ponto ( a , b ) nas duas funções nós podemos encontrar m e k :

b = m a → m = b a

b = k a 3 → k = b a 3

Passo 2

Agora vamos encontrar o elemento de área traçando linhas horizontais

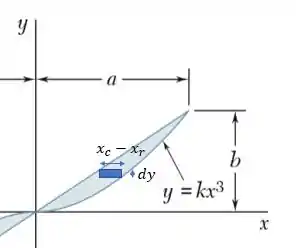
Onde x r é o x da reta e x c o x da equação cúbica, o que nos dá:

d A = x c - x r d y

Pois a curva mais a direita (no eixo positivo) é a função cúbica, no eixo negativo se colocaria a reta primeiro mas o ponto seria ( - a , - b ) o que vai acabar dando na mesma.

x r = y m ;     x c = y k 1 3

x r = a y b ;     x c = a y 1 3 b 1 3

Passo 3

Isso faz com que nossa integral de inércia em relação a x seja:

I x = ∫ y 2   d A

I x = ∫ y 2 × a   y b 1 3 - a b   y d y  

Como pegamos linhas horizontais não precisa do termo 1 / 3 .

Com y variando de - b a b :

I x = ∫ - b b a b 1 3   y 7 3 - a b y 3 d y

Fazendo a integral:

I x = a b 1 3 3 y 10 3 10 - b b - a b y 4 4 - b b

O que pode ser igual a:

I x = 2 a b 1 3 3 y 10 3 10 0 b - 2 a b y 4 4 0 b

I x = 6 a b 3 10 - 2 a b 4 4 b

I x = a b 3 10

Passo 4

Agora falta o raio de giro causado por essa inércia e que será calculado por:

k = I x A

Com isso falta apenas calcular a área ocupada por essa superfície e vamos calcular apenas integrando d A , que encontramos acima e foi dada por:

d A = x c - x r d y

d A = a   y b 1 3 - a b   y d y

Integrando em y temos:

A = 2 ∫ 0 b a b 1 3 y 1 3 - a b y d y  

Fazendo essa integral:

A = 2 × 3 a 4 b 1 3   y 4 3 - a y 2 2 b 0 b

A = 2 3 a b 4 - a b 2 = a b 2

Dessa forma podemos aplicar essa área encontrada na fórmula do raio de giro e ela será:

k = a b 3 10 a b 2 = b 2 5 = b 5

Resposta

I x = a b 3 10

k = b 5

Ver Outros Exercícios desse livro