Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 21
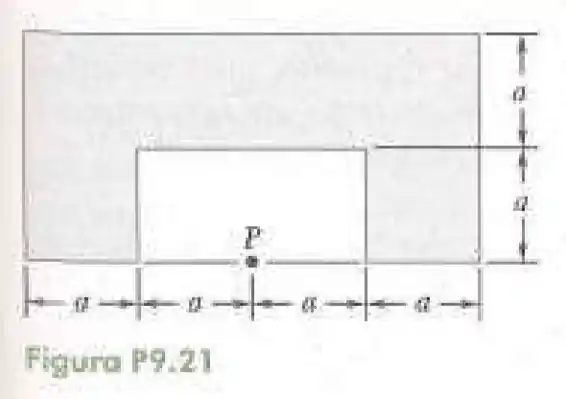
21- Determine o momento de inércia polar e o raio de giração polar da superfície sombreada mostrada na figura em relação ao ponto .
Passo 1
Para calcular o momento de inércia polar nós precisamos fazer a somatória da inércia em e em da figura ou seja:
E dessa forma vamos dividir a superfície em três regiões. Além de traçar nosso centro de coordenadas partindo de
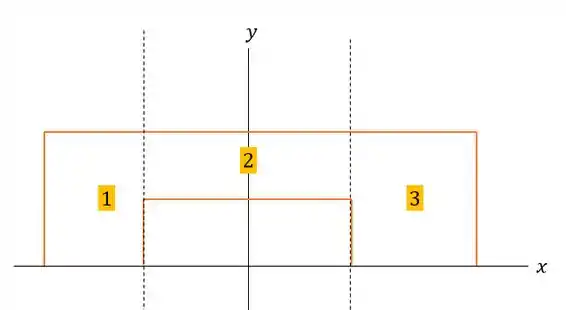
Onde as regiões e são iguais, tanto em área quanto em inércia em relação a e , podendo ser escrita da seguinte forma:
E a inércia total em e em do corpo todo pode ser escrito da seguinte forma:
Passo 2
Com isso dito vamos traçar as linhas verticais e horizontais para que seja possível calcular as inércias.
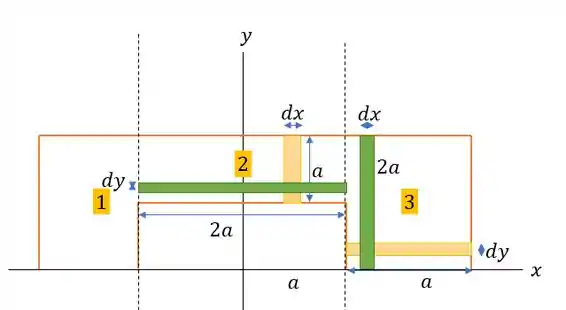
Vamos começar fazendo a inércia em .
O elemento de área na região vale (considerando o horizontal , verde):
E o elemento de área na região (na horizontal, o amarelo):
Porém como estamos considerando a inércia na região também então :
Onde na região varia de até e na região varia de até .
Passo 3
Agora vamos fazer a inércia em :
O elemento de área da região na vertical será:
E na região :
Porém como temos a região também então:
Fazendo a inércia em nós teremos:
Onde a região varia em de até e a região varia de até , o que nos dá:
O que nos dá:
Dessa forma a inércia polar vale:
Passo 4
Agora basta calcular o raio de giro polar e para isso vamos calcular a área dessa superfície que é fácil né? Basta fazer a soma das áreas das regiões:
Logo: