Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 22
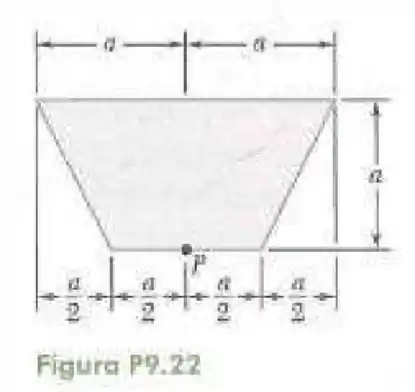
22- Determine o momento de inércia polar e o raio de giração polar da superfície sombreada mostrada na figura em relação ao ponto .
Passo 1
Fazendo o sistema de coordenada saindo de nós podemos dividir a seguinte superfície em quatro regiões.
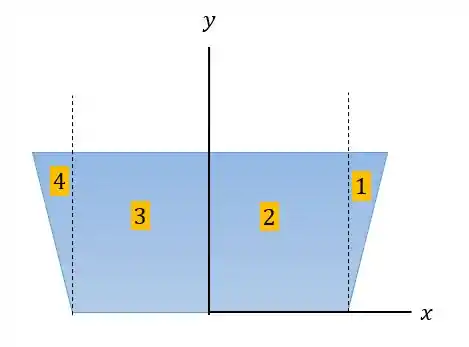
Onde a inércia nos eixos em é igual a inércia nos eixos em e a inércia em é igual a inércia em . E por isso vamos apenas traçar as linhas verticais e horizontais nas regiões e .
Mas antes vamos escrever a equação da reta diagonal que fecha o triângulo na região .
Essa reta passa pelos pontos e .
Sendo a equação da reta:
Substituindo esse valor de na primeira equação nós temos:
Logo:
Dessa forma a equação dessa reta diagonal será:
Passo 2
Agora vamos traçar as linhas para que possamos calcular as duas inércias.
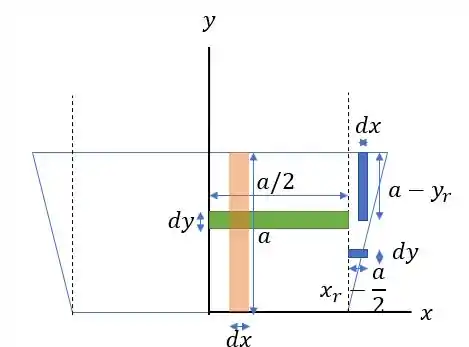
Onde é o da reta que acabamos de descobrir no passo anterior.
Fazendo a inércia em nós temos:
Onde na região vai de até e na região vai de até
Passo 3
Agora vamos fazer :
Para isso precisamos saber de , que vale:
Onde nas duas regiões vai de até .
Dessa forma a inércia polar será:
Passo 4
Para calcular o raio de giro nós precisamos saber a área dessa superfície e que será igual ao dobro das áreas da região com a soma do dobro da área da região
Dessa forma o raio de giro será: