2.26. A massa está ligada a uma corda que está sob uma tensão T, como mostra a figura 2.56. Supondo que T permaneça inalterada quando a massa for deslocada na direção normal à corda:
- Escreva a equação diferencial de movimento para pequenas vibrações transversais;
- Determine a frequência natural de vibração.

Passo 1
O primeiro passo é quase sempre desenhar o diagrama de forças, então vamos fazer isso:
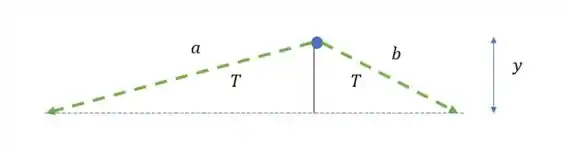
A gente pode dizer que a massa não se move no eixo , então
Toda a força resultante está em .
Passo 2
Então vamos usar as forças em . Nós não temos nem um ângulo para decompor as forças, mas temos uma coisa que podemos usar, um triângulo!
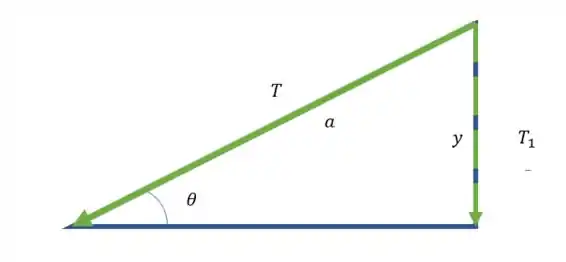
Este é o triângulo do lado esquerdo da imagem. A força é a componente em que estamos buscando.
Podemos dizer que
Mas
Então
E analogamente podemos fazer para o outro lado
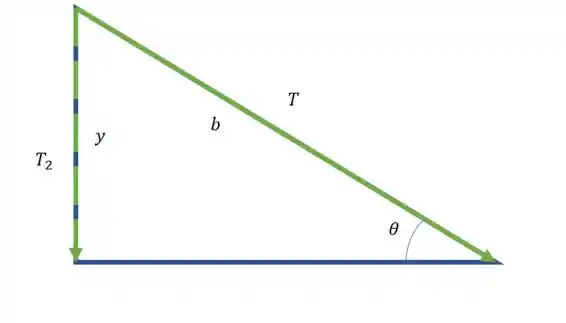
Então podemos fazer
Isso fica
Passo 3
Então sabemos que
E
Então a equação de movimento é:
Achamos a resposta do item (a).
Passo 4
Agora vamos para o item (b). Para descobrir a frequência natural de vibração podemos usar a equação:
A gente sabe que
E a força é
Então podemos concluir que
Então
Isso aqui também pode ser escrito assim