23- Determine a força em cada elemento da treliça e indique se esses elementos estão sob tração ou compressão.
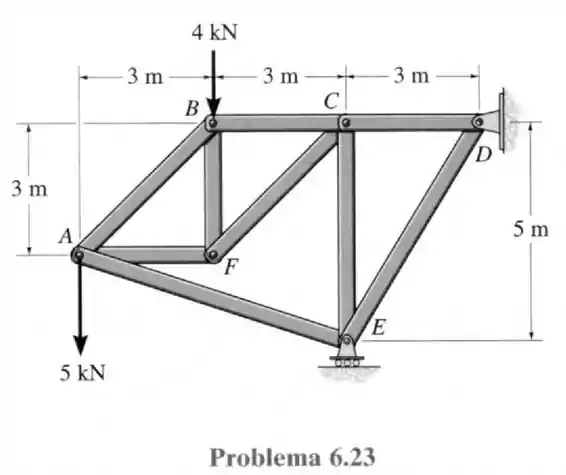
Passo 1
Existe somente reação vertical em e reações verticais e horizontais em , fazendo com que a estrutura equivalente seja a retratada abaixo.
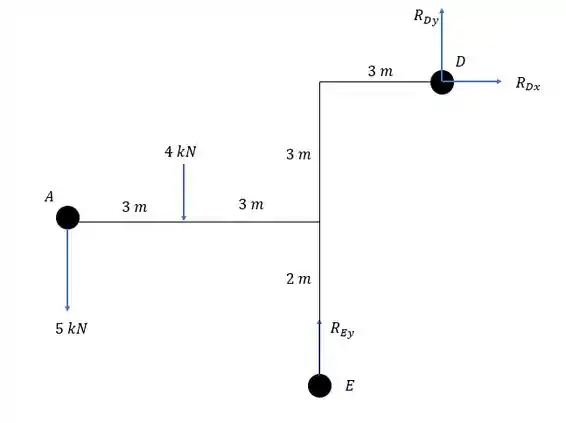
Onde separamos apenas as distâncias verticais e horizontais das forças ativas na estrutura (as forças de e de ) para os apoios.
Fazendo a somatória das forças horizontais temos:
E agora fazendo a somatória dos momentos em temos:
Logo pela somatória das forças verticais temos:
Logo:
Isso nos diz que o sentido da força em está ao contrário da do que foi desenhado na figura.
Passo 2
Agora estamos aptos a analisar os nós, o nó tem três incógnitas para uma força ativa somente, o nó a mesma coisa, assim como o nó , o melhor para começar é o nó pois só teremos três barras/incógnitas para o nosso problema.
Analisando o nó .
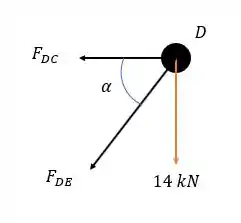
Onde vale:
Fazendo a somatória das forças verticais no sistema temos:
Força compressiva, pois consideramos a força saindo do nó de encontro com a barra.
Agora fazendo a somatória das forças horizontais:
Passo 3
Agora temos duas incógnitas na junta e é pra lá que nós vamos:
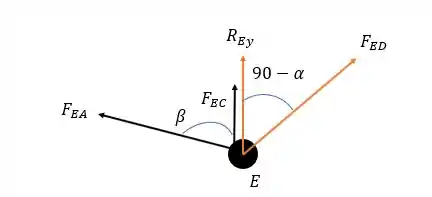
Onde pode ser calculado utilizando o triângulo de apoio abaixo:
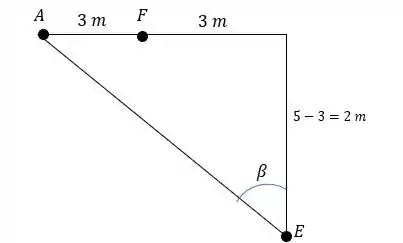
Logo pela somatória das forças horizontais temos:
Agora pela somatória das forças verticais:
Passo 4
Agora vamos para o nó :
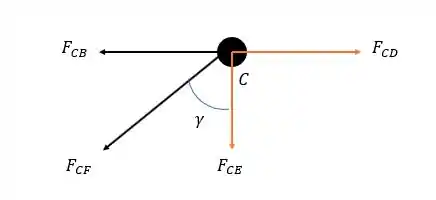
Onde vale:
Pela somatória das forças verticais temos:
Agora pela somatória das forças horizontais temos:
Passo 5
Indo para o nó teremos:
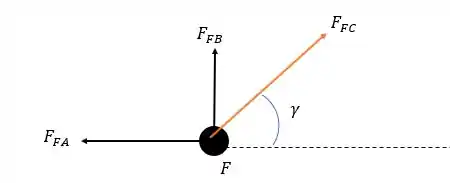
Fazendo a somatória das forças horizontais temos:
Agora a somatória das forças verticais:
Passo 6
Agora para fechar vamos analisar o nó .
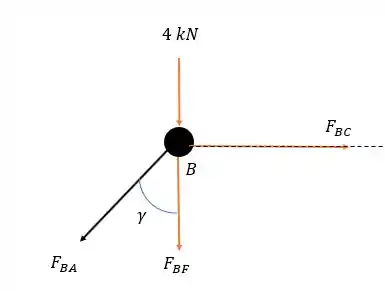
Analisando o ângulo formado entre e a vertical vemos que o ângulo entre eles é o mesmo que que vale .
Fazendo a somatória das forças horizontais vemos que:
Com isso encontramos todas as forças mas vamos ver se a somatória das forças na vertical será igual a zero:
Logo está certinho.
O mesmo raciocínio pode ser feito para o nó mas finalizaremos por aqui.