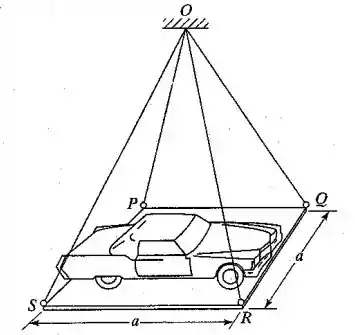
2.31. Uma plataforma quadrada PQRS e o carro que ela está suportando têm uma massa combinada M. A plataforma é suspensa por quatro cabos elásticos de um ponto fixo O, como indicado na Figura 2.61. A distância vertical entre o ponto de suspensão O e a posição horizontal de equilíbrio da plataforma é h. Se o lado da plataforma for a e a rigidez de cada cabo for k, determine o período de vibração vertical da plataforma.
Passo 1
Para esse problema aqui temos basicamente uma pirâmide de base quadrada:
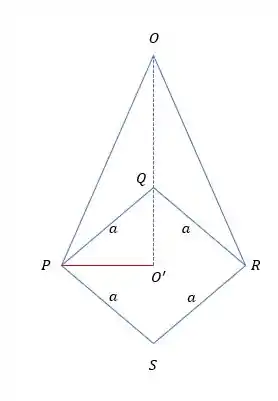
Essa linha pontilhada é a altura
A linha vermelha vai ser a metade da diagonal do quadrado de lado .
E as diagonais da pirâmide que são as cordas podem ser medidas por Pitágoras
Passo 2
Quando os fios se alongam a gente vai ter uma nova altura para o sistema, essa altura vai ser somado com o tamanho do esticamento das cordas.
Então os fios vão medir o seguinte
Em que é o quanto a corda esticou.
Agora podemos isolar
Mas nós conhecemos o valor de
Vamos mexer um pouquinho nessa equação. Podemos colocar em evidência.
Agora vamos desenvolver
Isso fica
Agora vamos fazer uma aproximação. Assumindo que é um valor pequeno, podemos desprezar da equação
e fazer a seguinte aproximação
Se considerarmos
Então
Chegamos numa expressão para a oscilação da corda.
Passo 3
A equação de movimento é dada por
Para calcular esse podemos usar a energia potencial do movimento.
Por outro lado, podemos calcular
Assim calculamos separadamente a energia potencial de cada corda e depois somamos.
Substituindo o valor de
Então
Logo
A equação de movimento fica assim
Agora podemos enxergar mais facilmente que
Mas o problema pede o período. Então basta fazer
Substituindo
Isso aqui vai dar
E terminamos mais um!