Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.4 - Ex. 33
33- A treliça de telhado sustenta o carregamento vertical mostrado na figura. Determine a força nos elementos e e indique se eles estão sob tração ou compressão.
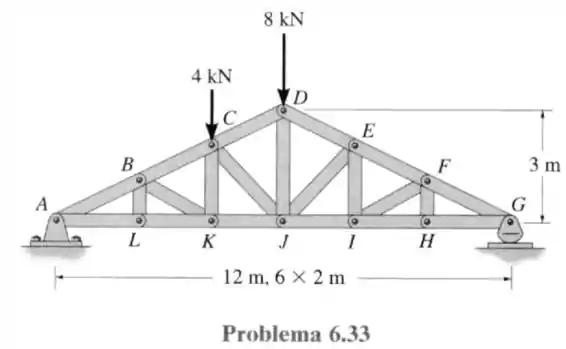
Passo 1
A figura nos diz que as barras e são iguais e tem tamanhos iguais a e com essa informação podemos calcular as reações verticais nos apoios em e sabendo que não há reações horizontais uma vez que não há forças ativas horizontais atuando na estrutura.
Para isso vamos fazer uso da estrutura equivalente.
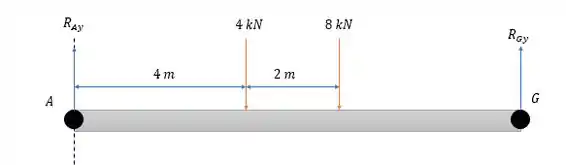
Fazendo a somatória das forças verticais temos:
Fazendo agora a somatória dos momentos em temos:
Dessa forma:
Passo 2
Agora podemos aplicar o corte nas barras ditas no enunciado, o que faz com que se observarmos a estrutura a sua esquerda tenhamos com a seguinte estrutura abaixo:
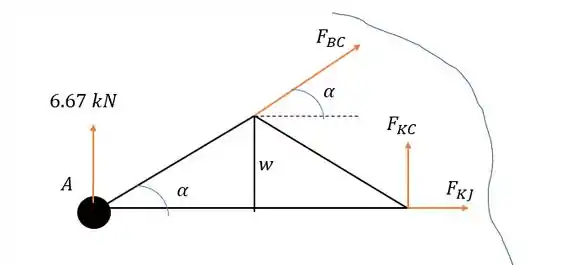
Onde tem o seguinte valor:
E o valor do comprimento da barra vale:
Passo 3
Fazendo a somatória das forças verticais no sistema temos que:
E a somatória dos momentos em nos dará:
Logo:
Compressiva, uma vez que a resposta é negativa e consideramos a força saindo do nó.
Passo 4
Para encontrar a última força basta fazer a somatória das forças horizontais e igualar a zero, isso é: