Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 2.3 - Ex. 13
13- A força de que atua na estrutura deve ser decomposta em dois componentes que atuem ao longo do eixo das escoras e . Se o componente da força ao longo de tiver de ser de , orientado de para determine a intensidade da força que atua ao longo de e o ângulo da força de .
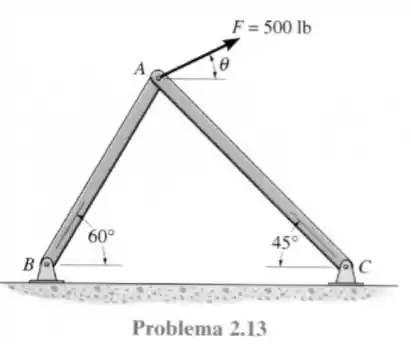
Passo 1
Vamos considerar que além de a força ir de até que a força terá sentido de para e com isso traçar os ângulos importantes para traçar o triângulo de forças.
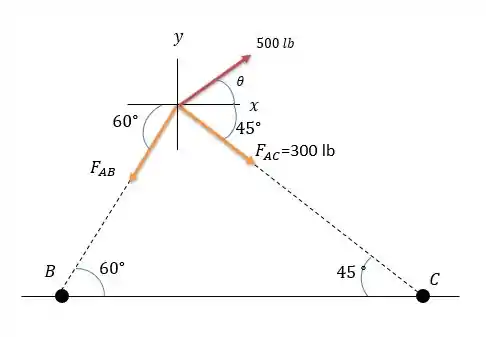
Passo 2
Tais forças se equilibram, isso faz com que surja o seguinte triângulo de forças.
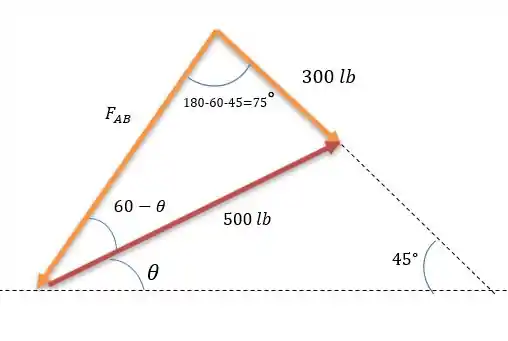
Pela lei dos senos temos:
Passo 3
Agora podemos preencher melhor nosso triângulo afim de pegar o outro ângulo que não conhecemos.
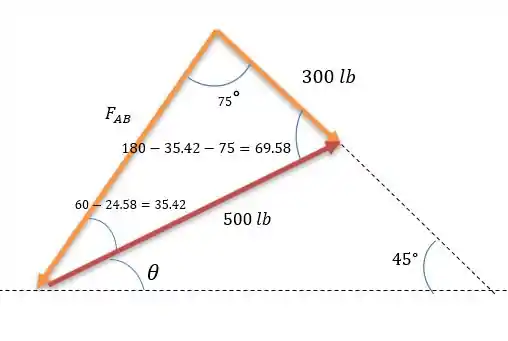
Diminuindo de encontramos uma ângulo de com isso vemos que o outro ângulo vale , logo pela lei dos senos temos: