34- Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo positivo.
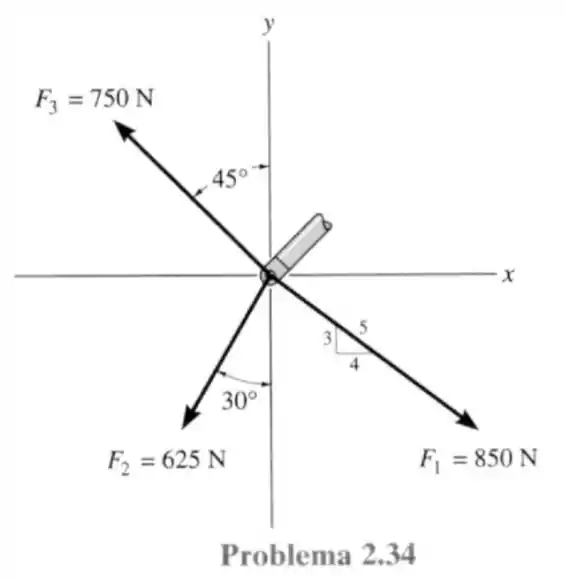
Passo 1
Assim como na questão passada o cosseno e o seno do triângulo retângulo são dados por:
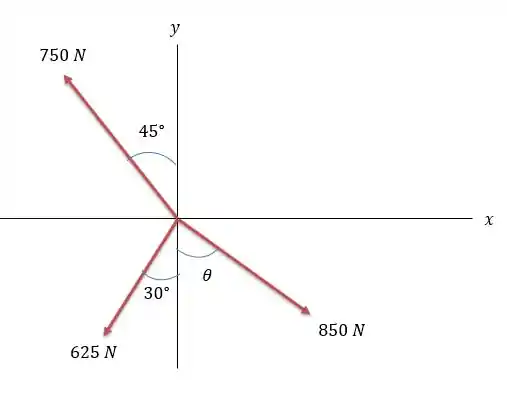
Fazendo a somatória de todas as projeções das forças na horizontal nós teremos a força :
Agora para a somatória das forças em temos :
Como as forças em e são negativas logo o ângulo da força resultante está no terceiro quadrante.
Passo 2
A força resultante será calculada por:
Logo:
Passo 3
O ângulo da força resultante que está no terceiro quadrante vale:
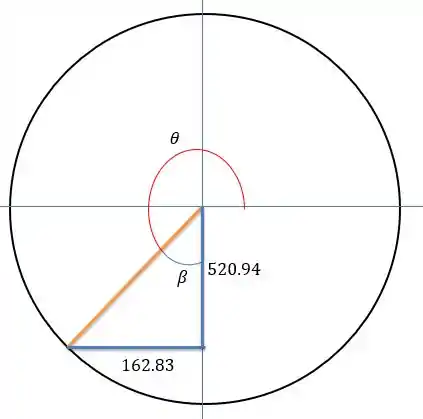
Onde vale:
Logo o ângulo que mede o ângulo da força resultante no eixo seguindo o sentido anti-horário será: