Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 2.4 - Ex. 51

51- Expresse cada uma das três forças que atuam sobre a coluna na forma vetorial cartesiana e calcule a intensidade da força resultante.

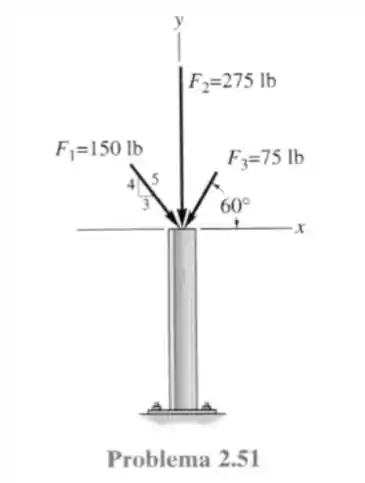
Passo 1

Como o eixo x aponta para a direita e o eixo y aponta para cima faz com que todas as forças tenham um componente F y para baixo e F 1 tenha um componente F x positivo. Logo:

F 2 = - 275 j ^   [ l b ]

F 3 = - 75 cos ⁡ 60 i ^ - 75 sin ⁡ 60 j ^ = - 37.5 i ^ - 64.95 j ^   [ l b ]

Agora F 1 pode ser representada da seguinte forma:

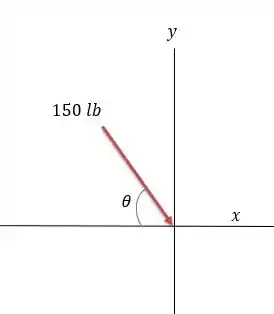
Onde θ está no triângulo retângulo de modo que ele tem os seguintes valores de seno e cosseno:

sin ⁡ θ = 4 5 ;   cos ⁡ θ = 3 5

O que nos dá então uma decomposição de forças em F 1 igual a:

F 1 = 150 cos ⁡ θ i ^ - 150 sin ⁡ θ j ^ = 90 i ^ - 120 j ^

Passo 2

Isso nos dá a seguinte somatória das forças:

F 1 + F 2 + F 3 = - 37.5 + 90 i ^ + - 120 - 64.95 - 275 j ^ = 52.5 i ^ + - 459.95 j ^

Logo a intensidade dessa força será:

F r = 52.5 2 + - 459.95 2 = 462.94   l b

Resposta

F 1 = 90 i ^ - 120 j ^   [ l b ]

F 2 = - 275 j ^ [ l b ]

F 3 = - 37.5 i ^ - 64.95 j ^   l b

F r = 462.94   l b

Ver Outros Exercícios desse livro