Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 4.4 - Ex. 17

4.17. uma força de 80   N atua sobre o cabo de um cortador de papel em A. Determine o momento criado por essa força em relação à dobradiça em O, se θ = 60 ° . Em que ângulo θ a força deve ser aplicada para que o momento criado em relação ao ponto O (no sentido horário) seja o máximo? Qual é esse máximo momento?

Passo 1

Vamos começar esquematizando o problema

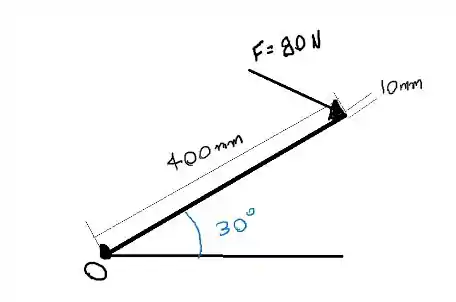
Passo 2

Vamos determinar o momento gerado pela força F

M = F ⋅ d = - 80 ⋅ cos ⁡ θ ⋅ 0,01 - 80 ⋅ sin ⁡ θ ⋅ 0,4

Então

M = 0,8 ⋅ cos ⁡ θ - 32 ⋅ sin ⁡ θ

Fazendo θ = 60 °

M = 0,8 ⋅ cos ⁡ 60 ° - 32 ⋅ sin ⁡ 60 ° = 28,1     N ⋅ m

No sentido horário.

Passo 3

Agora para determinar o ângulo que produz o momento máximo, vamos fazer o seguinte, temos M em função de θ , e sabemos que se derivarmos a função e igualar a 0 vamos obter um mínimo ou um máximo. Então

d M d θ = 0

A derivada de M em relação a θ fica

d M d θ = - 0,8 ⋅ sin ⁡ θ + 32 ⋅ cos ⁡ θ

Se igualarmos a 0

- 0,8 ⋅ sin ⁡ θ + 32 ⋅ cos ⁡ θ = 0

0,8 ⋅ sin ⁡ θ = 32 ⋅ cos ⁡ θ

Então

sin ⁡ θ cos ⁡ θ = 32 0,8

Logo temos

tan ⁡ θ = 32 0,8

Daqui podemos determinar θ

θ = t a n - 1 32 0,8 = 88,6 °

Como disse antes, temos um ponto, mas não sabemos se é mínimo ou máximo, pode até ser de inflexão, para descobrirmos isso vamos fazer a segunda derivada

d 2 M d θ 2 = - 0,8 ⋅ cos ⁡ θ - 32 ⋅ sin ⁡ θ

Para θ = 88,6 ° temos

- 0,8 ⋅ cos ⁡ 88,6 ° - 32 ⋅ sin ⁡ 88,6 ° = - 32,0

É um número negativo, por tanto concluímos que é um ponto de máximo.

Passo 4

Agora vamos determinar o momento para o ângulo que maximiza o momento

M m a x = 0,8 ⋅ cos ⁡ 88,6 ° - 32 ⋅ sin ⁡ 88,6 ° = 32,0   N ⋅ m

O sentido é horário.

Resposta

M = 28,1     N ⋅ m

θ = 88,6 °

M m a x = 32,0   N ⋅ m

Ver Outros Exercícios desse livro