4.19. O cubo de roda na figura pode ser fixado ao eixo tanto com um afastamento negativo (para a esquerda) como com um afastamento positivo (para a direita). Se o pneu está sujeito às cargas normal e radial, como mostrado, determine o momento resultante dessas cargas em relação ao eixo no ponto O em ambos os casos.
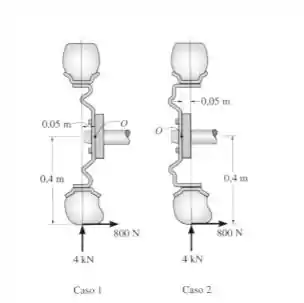
Passo 1
Fala aí, bora resolver esse probleminha de momento?
Bom aqui são 2 casos e a gente vai desenhar o diagrama de corpo livre de cada caso e assim resolver, beleza?
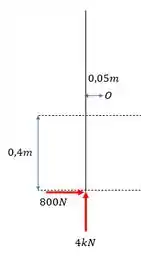
Esse é o diagrama de corpo livre do caso 1. E pra calcular o momento em relação ao eixo O, a gente vai usar a equação:
Onde a força precisa ser perpendicular a distância.
Passo 2
Vamos definir como positivo aqui o sentido anti-horário. Assim para o primeiro caso a gente tem.
Se você tiver alguma dúvida pra onde a peça vai girar com cada uma das forças, você pode usar a regra da mão direita e direcionar a mão no sentido da força envolvendo o eixo de interesse. Traçar uma linha do eixo até as forças também ajuda nessa visualização.

Passo 3
Para o segundo caso, o DCL fica desse jeitinho:
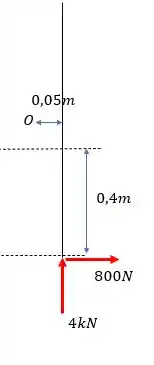
E aí tomando o sentido anti-horário como positivo a gente vai ter:
E o sentido continua sendo anti-horário, e da mesma forma a gente pode usar aquelas dicas pra visualizar o sentido dos momentos.
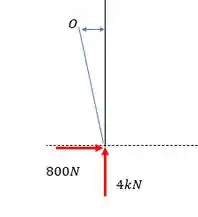
Resposta
O sentido é anti-horário para os dois casos.