Como a intensidade do momento de binário resultante é igual a determine a intensidade das forças aplicadas sobre as chaves:

Passo 1
Aqui podemos aproveitar os resultados que encontramos para a questão , vamos repeti-los aqui.
A definição do momento de binário é a seguinte:
Onde e são os vetores que ligam a origem do sistema de coordenadas até os dois pontos de aplicação das forças e .
Já temos a intensidade do momento e quremos calcular a força, então falta encontrar os dois vetores e .
Passo 2
Começamos por , o seu módulo é:
Agora vamos procurar os ângulos diretores. Confiar no desenho pode ser um pouco arriscado: não podemos garantir que passa por cima do eixo , apesar de parecer assim:
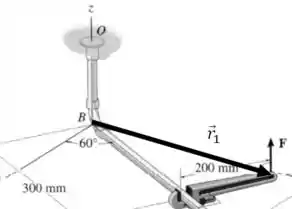
O ângulo que forma com o segmento é:
E como o eixo forma um ângulo de com esse mesmo segmento, o ângulo entre e o eixo é:
Então podemos escrever o vetor da seguinte forma:
Passo 3
Agora vamos procurar uma expressão como essa para . Mais uma vez, começamos pelo módulo:
E mais uma vez vamos procurar o ângulo em relação ao eixo :
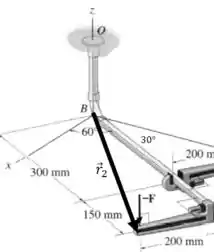
E então as componentes do vetor são:
Passo 4
E agora vem a mudança em relação à questão anterior, vamos aplicar a fórmula que aplicamos no primeiro passo:
Vamos reescrever esse produto vetorial como o determinante de uma matriz:
E o módulo de deve ser igual a , então:
Resposta
A intensidade de cada uma das forças deve ser de .