4.49. A força dá origem a um momento em relação ao ponto O de . Considerando que a força atua em um ponto com coordenada x igual a 1 m, determine as coordenadas y e z desse ponto. Além disso, considere e encontre a distância perpendicular do ponto O até a linha de ação da força F.
Passo 1
Bem, nós sabemos que
Isso pode ser representado pela matriz
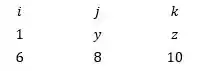
Passo 2
Agora fazendo o determinante dessa matriz, chegamos no seguinte sistema linear
Daqui podemos tirara que
Logo
Passo 3
Para determinar , vamos usar
Sabemos que
E também temos
Então