Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 45
45- Determine o momento de inércia polar da área mostrada na figura em relação ao ponto , ao centroide da superfície.
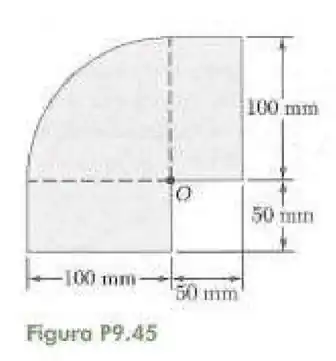
Passo 1
Vamos traçar o eixo de coordenadas partindo de:
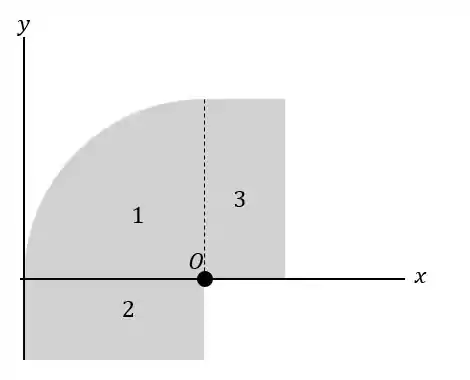
Para podermos encontrar a posição do centro da superfície nós dividimos a superfície em regiões e cujo eixo horizontal passa em para que sejamos capazes de descobrir a inércia nesse eixo:
Fazendo uma tabela para nos auxiliar nessa tarefa nós temos:
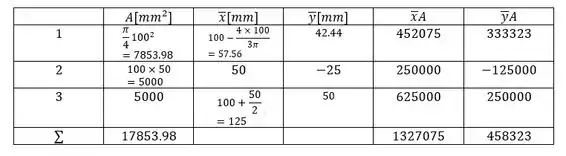
Isso nos dá:
Passo 2
As inércias polares (para um centro) de um retângulo e de um quarto de círculo são calculados por:
E para calcular a inércia no ponto nós devemos considerar a distância (no caso de uma linha reta ) do centro da região até(isso somente para os retângulos para o semicírculo não). A figura da página nos mostra apenas a inércia polar no centro no caso do retângulo.
Logo as inércias polares em relação a de cada região serão iguais a:
Então a inércia será:
Passo 3
Agora para calcular a inércia no ponto nós precisamos da distância entre e (que é o centroide) e ela vai ser dada por:
E ela será calculada por:
Logo: