Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 5.4 - Ex. 57
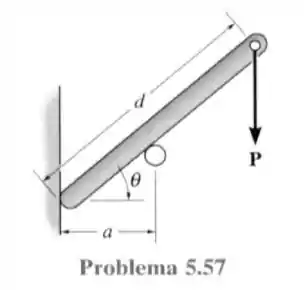
57- Determine a distância para a colocação da carga de modo que a barra da lisa seja mantida em equilíbrio na posição , como mostrado na figura. Despreze o peso da barra.
Passo 1
Essa bolinha branca presente na figura é uma espécie de apoio e ela faz apoio em um direção que seja perpendicular a barra, pois o apoio é circular. Além de ter um contato normal com a parede, ficando da seguinte maneira o diagrama de forças.
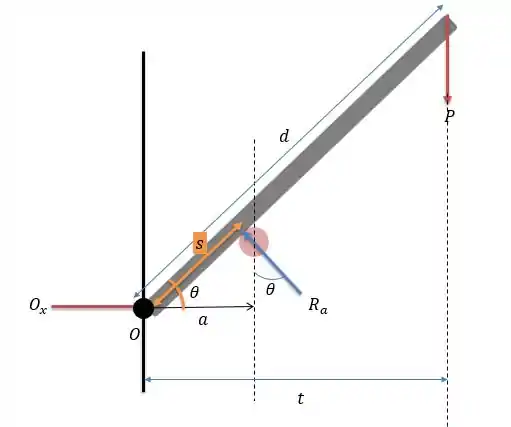
Passo 2
Fazendo a somatória das forças verticais temos:
E fazendo agora a somatória dos momentos em temos:
Onde temos que sempre fazer a multiplicação entre a força e a distância perpendicular a essa distância. Como a força no apoio é perpendicular a barra, então a distância é a distância de comprimento marcada na figura, que será calculada com o triângulo formado entre eles:
A distância a da força é marcada pela distância igual a e ela será calculada por:
Logo:
Passo 3
Substituindo o valor de encontrado na somatória das forças verticais temos:
Isolando temos: